見かけの大きさの計算

　まずは、系外惑星がその中心星を隠すという状況を簡素化して考えてみたいと思います。 以下の図のような状況を考えます。

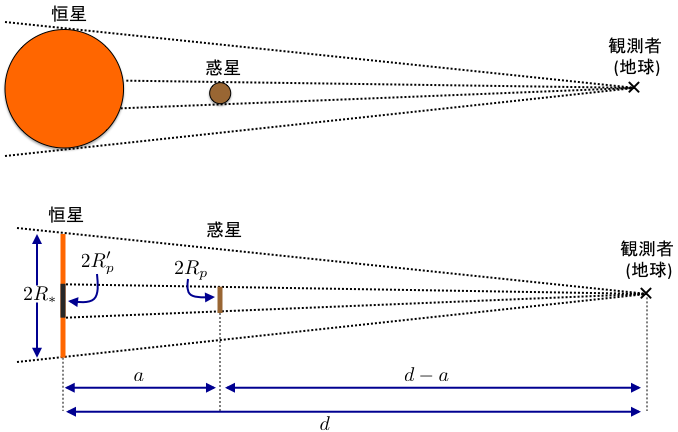
　図の上のイラストが、観測者 (地球) から見て惑星が恒星の手前を横切っている様子を表しています。 黒い点線で示したのが、恒星と惑星のそれぞれの見かけの大きさを表したものです。 この図では惑星は恒星の一部のみを隠していますが、それがどの程度の割合になるのかは、恒星・惑星・地球の 3 者のそれぞれの距離の関係によって変化しそうです。

　上のイラストの状況を簡略化したのが下のイラストです。 ここで、惑星の軌道長半径を \(a\) 、恒星までの距離を \(d\) とします。 恒星を半径 \(\Rstar\)、直径 \(2\Rstar\) の円盤と考え、同様に惑星を直径 \(2\Rp\) の円盤としています。 地球から見た場合、惑星は本来の自身の大きさである \(2\Rp\) 分ではなく、\(2\Rpp\) 分に相当する部分を隠していることになります。 そのため、3 者の距離の関係による違いは、惑星によって隠される部分の半径 \(\Rpp\) がどう表されるかという問題に帰着されることが分かります。

　式 \eqref{eq:3} を、身近な例で検算してみたいと思います。

　系外惑星のトランジットは系外惑星がその中心星を隠すという現象ですが、天体が別の天体を隠すという現象の身近な例として、日食があります。 トランジットの場合は、系外惑星は中心星の周りを公転していて、それを地球から観測するという状況になります。 対して日食の場合は、地球が太陽の周りを公転していて、さらに地球の周りを月が公転しているという状況であるため、3 者の位置関係は大きく異なります。 しかし、ある天体が別の天体を隠すという現象としては類似しています。 そのため、恒星までの距離 \(d\) を "地球から太陽までの距離"、惑星までの距離 \(d-a\) を "地球から月までの距離" と読み替えれば、月食の際の計算にも用いることができます。

　まず、\(\Rp\) を月の半径とし、地球から太陽までの距離 \(d\) と地球から月までの距離 \(d-a\) から、月が太陽を隠す時の見かけの半径に対応する \(\Rpp\) を計算します。 月の平均半径は 1737.15 km、地球から太陽までの距離は \(d\) = 1 AU = 149597879.700 km です。 また地球から月までの距離は、平均的な値 (月の軌道長半径) を用いると \(d-a\) = 384400 km です。 これを用いると、 \begin{align*} \Rpp=6.76\times10^{5}\,{\rm km} \end{align*} となります。 一方、太陽の半径は \begin{align*} \Rsun=6.96\times10^{5}\,{\rm km} \end{align*} であるため、非常に近い値になっていることが分かります。 つまり、太陽・地球・月の位置関係で月が太陽を隠す際は、見かけの大きさは非常に近い値になるため、一直線に重なった場合は太陽の大部分あるいはすべてを隠す、金環日食または皆既日食になるということになり、事実と合致しています。

　次に本題であるトランジット時の減光率を計算してみます。 減光率を計算するときは、恒星と惑星の断面積の比から求められることになりますが、正確には惑星が恒星を隠す見かけの半径 \(\Rpp\) を用いて断面積を計算する必要があることになります。 そのため、トランジット時の減光率は以下のように計算できます。 \begin{align*} \frac{\Delta L}{L}&=\frac{\pi{\Rpp}^{2}}{\pi\Rstar^{2}}\\ &=\left(\frac{d}{d-a}\right)^{2}\left(\frac{\Rp}{\Rstar}\right)^{2}\\ &=\left[\frac{1}{1-\left(\frac{a}{d}\right)}\right]^{2}\left(\frac{\Rp}{\Rstar}\right)^{2}\\ &=\left[1-\left(\frac{a}{d}\right)^{-2}\right]\left(\frac{\Rp}{\Rstar}\right)^{2} \end{align*}

　\(L\) が恒星の本来の光度、\(\Delta L\) がトランジットによる光度の変化分であり、\(\Delta L/L\) が減光率となります。 減光率が、惑星の半径、恒星の半径と、惑星の軌道長半径 \(a\) 、恒星までの距離 \(d\) を用いて表されていることが分かります。

　ここで係数部分を考えてみます。 惑星の軌道長半径 \(a\) は惑星によって様々ですが、おおむね AU (天文単位) で表すことのできる程度の大きさです。 また恒星までの距離 \(d\) も様々ですが、発見されている系外惑星の大部分は数十光年から数千光年の距離にあり、そもそも一番近い恒星までの距離が 4 光年程度なので、おおむね pc (パーセク) で表すような距離だという事が分かります。

　pc と AU には

誤差の評価

　直感的にも分かることではありますが、系外惑星の軌道長半径がその惑星系までの距離に比べて遥かに小さいため、軌道長半径と恒星までの距離の影響は減光率にほとんど影響を及ぼさないということが分かりました。 減光率の係数部分は、 \begin{align*} \frac{a}{d}\ll 1 \end{align*} として展開すると以下のようになります。 \begin{align} \left[1-\left(\frac{a}{d}\right)\right]^{-2}\simeq1+2\left(\frac{a}{d}\right)+o\left(\left(\frac{a}{d}\right)^{2}\right) \label{eq:5} \end{align} よって、\(a/d\) の 1 次の誤差があることになります。

　例えば、10 pc の距離にある恒星が、軌道長半径 1 AU の惑星を持っていたとします。 つまり a = 1 AU、d = 10 pc という状態です。 この惑星のトランジットによる減光率をそのまま恒星と惑星の半径比に焼き直した際の誤差は、式 \eqref{eq:5} より 9 × 10^-7、つまりおよそ 0.0001% になることが分かります。

　具体的な例として、ホットジュピターの典型例である HD 209458b の場合を考えてみます。 HD 209458b の軌道長半径は a = 0.045 AU、中心星である HD 209458 までの太陽系からの距離は d = 47.1 pc (= 154 光年) です。 この値から、式 \eqref{eq:5} での誤差を計算すると 9 × 10^-9となり、およそ 0.000001% の誤差という極めて小さい値となることが分かります。

　これまでの観測から、HD 209458b のトランジットに伴う減光率はおよそ 1.5% であることが分かっています。 式 \eqref{eq:4} の減光率と惑星半径・恒星半径の関係を用いると、\(\Delta L/L=0.015\) を代入することで、HD 209458b の半径は中心星である HD 209458 のおよそ 0.1225 倍であると計算することができます。 別の観測から、HD 209458 の半径は太陽の 1.14 倍であることが分かっています。 また木星半径は太陽半径の 0.103 倍であることも用いると、HD 209458b の半径は木星半径の 1.36 倍であることが分かります。 この値に対して 0.000001% の誤差があるということになりますが、その他の観測誤差に完全に埋もれてしまうほどの小さな誤差にすぎません。 そのため、惑星の軌道長半径や恒星までの距離の影響を無視することによる誤差は無視できるということが分かります。

　なお、HD 209458b の半径のデータは、2017 年 6 月時点では 1.35 ± 0.05 木星半径 となっています。

参考文献