天体の見かけの大きさ - 物理のメモノート

　夜空の恒星は点にしか見えませんが、太陽や月は一定の大きさを持って見えます。天体が大きいほど見かけの大きさは大きくなり、また天体までの距離が近いほど見かけの大きさは大きくなります。太陽や月の見かけの大きさは、日食などの現象を考える時に重要です。太陽と月と地球の 3 者が一直線に並ぶと、太陽が月に隠されて日食が発生しますが、太陽と月の見かけの大きさがほとんど同じである為に、微妙な距離の差で、月が太陽を全て隠す皆既日食になったり、完全には隠しきれない金環日食になったりします(特殊な場合は、金環皆既日食となることもあります)。

　ここでは、まず天体の見かけの大きさの指標である視直径の計算について簡単に紹介し、それから具体的な計算例も紹介します。

目次：

天体の見かけの大きさと視直径
視直径の計算
月・太陽の視直径と日食

天体の見かけの大きさと視直径

　空に見える天体の見かけの大きさを表す時に、通常大きさを表すような単位 (センチメートルやメートルなど) を用いる事は出来ません。空に定規を当てて大きさを測定する事は出来ないことや、見かけの大きさは天体の本当の大きさとその天体までの距離によって変わってしまうので、単純に長さで表すことができないためです。

　同じ大きさの天体でも、観測者 (例えば地球上) からの距離が遠ければ小さく見えますし、逆に近ければ大きく見えます。また、天体の大きさが違っても、それぞれの天体までの距離によっては見かけの大きさが一緒になることもあります。その模式図が以下の図になります。

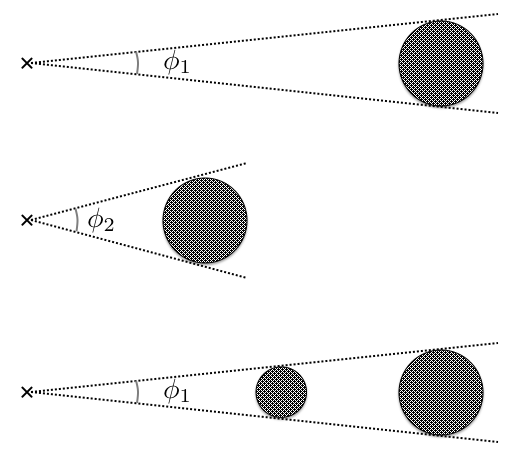
　上の 2 つは、天体の大きさが同じで、距離が異なる場合の例です。中段の図の方が天体までの距離が近いため、見かけの大きさは大きくなります。一番下の図は、天体の大きさが異なるにもかかわらず、距離が異なるため見かけの大きさが等しくなる例です。小さい天体が近距離に、大きい天体が遠距離にあるため見かけの大きさが同じになっています。

　このように、見かけの大きさを評価する時には、天体の大きさとその天体までの距離の両方が必要となります。図にも示したように、観測者から見てその天体を見込む角度が何度になるのかという点が重要です。小さい天体であっても近距離にあればその天体を見込む角度は大きく (見かけの大きさが大きく)、大きくても遠方であればその天体を見込む角度は小さく (見かけの大きさが小さく) なります。

　図中で $\phi$ を使って表しましたが、ある天体の見かけの大きさを表す時は、角度を用いて表します。見かけの大きさの直径は視直径 (apparent diameter) と呼ばれます。半径の場合は視半径 (apparent radius) と呼びます。角度であるため表記は度になりますが、一般に天体の見かけの角度は度より小さいため、それより細かい単位である分や秒もしばしば使われます。

　天体の見かけの大きさが何度になるのかは、幾何学的に求めることができます。

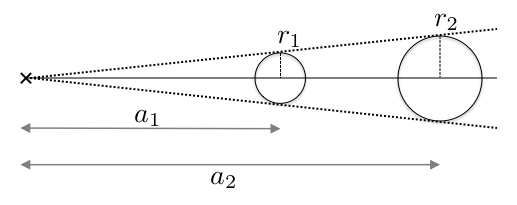
　上の図は、大きさが異なるが距離が違うため見かけの大きさが等しくなる例の模式図です。半径 $r$ がそれぞれ異なり、観測者から天体までの距離 $a$ も異なりますが、両者を見込む角度は等しくなっていることが分かります。天体までの距離と天体の実際の半径から視半径が計算出来、それを 2 倍すれば視直径となります。図は相似形になっているため、天体までの距離と天体の実際の半径の比率が同じであれば、見かけの大きさ、つまり視直径も等しくなります。

視直径の計算

視直径の概算方法

　まずはおおまかに視直径を計算する方法を考えます。上でも述べたように、天体の実際の大きさとその天体までの距離から、まずは視半径を計算します。

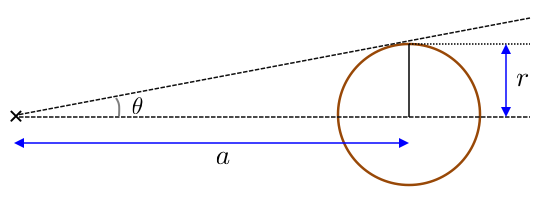
　上図のような状況を考えます。天体間の距離 (正確には観測者から天体までの距離) を $a$ 、天体の半径を $r$ とし、観測者からその天体の半径を見込んだ視半径を $\theta$ とします。図では書いていませんが、視直径 $\phi$ は視半径 $\theta$ の 2 倍の値となります。このとき、視半径 $\theta$ は次のような関係にあることがすぐに分かります。

$\begin{align*} \tan\theta=\frac{r}{a} \end{align*}$ タンジェントの逆関数を用いて

$\theta$ を求めると、次のようになります。

$\begin{align*} \theta=\arctan\left(\frac{r}{a}\right) \end{align*}$ ここで、

$\arctan$ はタンジェントの逆関数を表す関数で、アークタンジェントと読みます。場合によっては

${\rm Tan^{-1}}$ と表記されることもありますが同じものです。この式の

$r$ と

$a$ に実際の値を代入し、アークタンジェントを計算すれば視半径が求まることになります。

　一般に、アークタンジェントを含む三角関数の値は手計算出来ませんが、ここで近似を用いると式が簡単になります。天体までの距離と天体の半径では、大抵の場合天体までの距離の方が圧倒的に大きな値となります。例えば地球と月との距離はおよそ 38万 km ですが、月の半径はおよそ 1700 km であり、224 倍もの違いがあります。つまり、 $r\ll a$ という関係になっています。この場合、 $\theta\ll1$ であり、視半径は非常に小さい値となります。

　 $\theta$ が微小である場合、 $\tan\theta\approx\theta$ と近似することができます。そのため、視半径は $\arctan$ を使わずに近似的に

$\begin{align*} \theta\approx\frac{r}{a} \end{align*}$ と表すことができます。従って、視直径はこれを 2 倍して

$\begin{align*} \phi=2\theta\approx\frac{2r}{a} \end{align*}$ と表すことができる事が分かります。

　天体の見かけの大きさ (視直径)

$\phi$ は、天体までの距離を

$a$ 、天体の半径を

$r$ とすると、

$\begin{align*} \phi\approx\frac{2r}{a} \end{align*}$ で求めることができる。ただし、

$r\ll a$ であるとする。

　実際にこの式を使って、身近な天体の視直径を計算してみます。

　まずは月の見かけの大きさを計算します。地球と月の平均的な距離はおよそ 384400 km です。月の半径は 1737.15 km となので、これを代入すると
$\phi$ = 9.038...× 10^-3 [rad]
という値になります。 ここでの角度の単位はラジアン [rad] になっています。そこで度になおすために $360/2\pi$ をかけると、
$\phi$ = 0.51785... [度]
となります。角度の単位は 1 度 = 60 分、1 分 = 60 秒であるため、この値は 31.07 分ということになります。

　次に太陽の見かけの大きさを計算します。地球と太陽の平均的な距離は 1 AU であり、これは 1.49597870700 × 10⁸ km です。また、太陽の赤道半径は 6.96 × 10⁵ km であるため、代入すると
$\phi$ = 9.304...× 10^-3 [rad]
となり、度に直すと
$\phi$ = 0.53313... [度]
になります。分で表すと 31.99 分です。

　月の視直径はおよそ 31 分、太陽の視直径はおよそ 32 分となり、太陽と月の視直径は非常に近いという事が分かります。視直径の計算から分かる事については後ほど紹介します。

観測者のいる天体の大きさを考えた場合

　ここからは、少し細かい話まで取り入れた場合にどうなるかを考えてみます。上では、観測者から天体までの距離を単に $a$ と起きましたが、実際に $a$ に代入した値は天体間の距離です。天体間の距離と言った場合は、天体の中心の間の距離を指す場合が多いため、観測者が乗っている天体の大きさを考慮した場合に式がどう変わるかを考えてみます。

　考えるのは以下の図のような状況です。

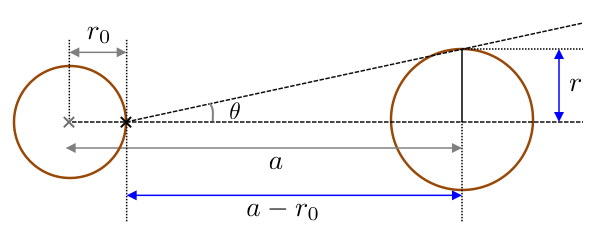
　天体間の距離を $a$ とし、観測者がいる天体の大きさを $r_{0}$ とします。この場合、観測者から対象の天体までの距離は $a-r_{0}$ となるため、天体を見込む角度に関して

$\begin{align*} \tan\theta=\frac{r}{a-r_{0}} \end{align*}$ という式になる事が分かります。従って、

$\theta$ は

$\begin{align*} \theta=\arctan\left(\frac{r}{a-r_{0}}\right) \end{align*}$ となります。先程と同様に

$r\ll a-r_{0}$ であるとすると、視直径は

$\begin{align*} \phi=2\theta\approx\frac{2r}{a-r_{0}} \end{align*}$ になります。

　観測者がいる天体の半径 $r_{0}$ が、天体間の距離より十分に小さい場合、つまり $r_{0}\ll a$ の極限を考えると、 $\displaystyle{\frac{r_{0}}{a}\ll 1}$ より、

$\begin{align*} \phi=\frac{2r}{a\left(1-\frac{r_{0}}{a}\right)}\simeq\frac{2r}{a} \end{align*}$ と近似でき、上で求めた視直径の式と一致することが分かります。

　一般に、観測者のいる天体の大きさと観測している天体までの距離では後者の方が遥かに大きいため、観測者がいる天体の大きさは無視出来ます。しかし、非常に近接した天体の見かけの大きさを考える場合は、観測者のいる天体の大きさが無視出来なくなる可能性があります。また、観測者がいる天体のどの位置から観測するかによって距離が変わり、見かけの大きさも変化します。ここで計算したのは、観測する天体に一番近い位置から見た時の見かけの大きさであるため、見かけの大きさの最大値に対応しています。

視直径のより厳密な表式

　次に、天体までの距離が非常に近く、天体までの距離と観測している天体の半径の比があまり大きくならないような状況での見かけの大きさについて考えてみます。考えるのは以下の図のような状況です。ここでは再び、観測者のいる天体の大きさは無視する事とします。

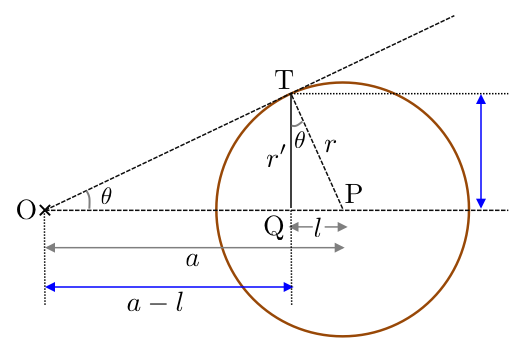
　一番初めの例では、天体までの距離を $a$ とし、天体の半径を $r$ として計算しました。しかし厳密には、図のように天体の半径 $r$ 分をその天体の大きさとして認識するのではなく、図中の $r^{\prime}$ の部分を大きさとして認識することになります。天体までの距離が遠い場合はこの効果は無視出来ますが、図のように天体に近くなるとこのずれは大きくなって無視出来なくなりそうです。そこで、ここではこの効果も含めて見かけの大きさを計算してみたいと思います。

　図より、先程までと同様に視半径について以下の式が成り立ちます。

$\begin{align*} \tan\theta=\frac{r^{\prime}}{a-l} \end{align*}$ ここで、

$r^{\prime}$ と

$l$ を、

$r$ と

$a$ を使って表します。

　図中の相似な三角形をそれぞれ取り出して描くと、以下のようになります。

相似の関係より、

$\begin{align*} {\rm PT:OP=PQ:PT} \end{align*}$ となるため、

$r:a=l:r$ から

$\begin{align*} l=\frac{r^{2}}{a} \end{align*}$ となる事が分かります。また、三角形 PQT から、

$\begin{align*} r^{2}=r^{\prime 2}=l^{2} \end{align*}$ となる事が分かるため、

$\displaystyle{l=\frac{r^{2}}{a}}$ を用いると

$\begin{align*} r^{\prime 2}=r^{2}-l^{2}=r^{2}-\frac{r^{4}}{l^{2}}=r^{2}\left(1-\left(\frac{r}{a}\right)^{2}\right) \end{align*}$ となり、

$\begin{align*} r^{\prime}=r\sqrt{1-\left(\frac{r}{a}\right)^{2}} \end{align*}$ と書き表すことができます。

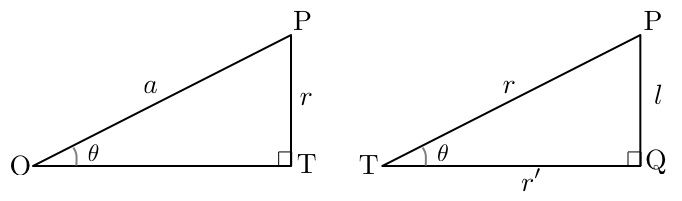
　これらの結果を用いると、 $\tan\theta$ は

$\begin{align*} \tan\theta=\frac{r^{\prime}}{a-l}=\frac{r\sqrt{1-\left(\frac{r}{a}\right)^{2}}}{a-\frac{r^{2}}{a}}=\frac{r}{a\sqrt{1-\left(\frac{r}{a}\right)^{2}}} \end{align*}$ となり、

$\begin{align*} \theta=\arctan\left(\frac{r}{a\sqrt{1-\left(\frac{r}{a}\right)^{2}}}\right) \end{align*}$ と表されます。

　従って、視直径は

$\begin{align*} \phi=2\arctan\left(\frac{r}{a\sqrt{1-\left(\frac{r}{a}\right)^{2}}}\right) \end{align*}$ という式で計算出来ることになります。これが、視直径のより厳密な表式です。

　視半径の式

$\begin{align*} \theta=\arctan\left(\frac{r}{a\sqrt{1-\left(\frac{r}{a}\right)^{2}}}\right) \end{align*}$ において、天体の大きさが天体間の距離に比べて十分小さい場合、つまり

$r\ll a$ である時は、平方根の中を 1 と近似して良いため

$\displaystyle{\theta=\arctan\left(\frac{r}{a}\right)}$ となり、さらに近似して

$\displaystyle{\theta\approx\frac{r}{a}}$ となります。そのため、

$r\ll a$ という状況においては、最初に求めた視直径の式と一致します。

　しかし、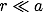では無い状況では、最初に求めた視直径の式では誤差が大きくなってしまいます。

　天体の視直径

$\phi$ のより厳密な表式は、天体までの距離を

$a$ 、天体の半径を

$r$ としたとき、

$\begin{align*} \phi=2\arctan\left(\frac{r}{a\sqrt{1-\left(\frac{r}{a}\right)^{2}}}\right) \end{align*}$ で与えられる。

誤差の評価

　下に、視直径の具体的な計算例をいくつか示します。

$\displaystyle{\phi=2\arctan\left(\frac{r}{a\sqrt{1-\left(\frac{r}{a}\right)^{2}}}\right)}$ (度) $\displaystyle{\phi\approx\frac{2r}{a}}$ (度) 誤差 (%)

地球から見た月 0.51785485 0.5178530873 0.00034

月から見た地球 1.901441735 1.901354481 0.0046

イオから見た木星 19.0855322 18.99741637 0.46

	$\displaystyle{\phi=2\arctan\left(\frac{r}{a\sqrt{1-\left(\frac{r}{a}\right)^{2}}}\right)}$ (度)	$\displaystyle{\phi\approx\frac{2r}{a}}$ (度)	誤差 (%)
地球から見た月	0.51785485	0.5178530873	0.00034
月から見た地球	1.901441735	1.901354481	0.0046
イオから見た木星	19.0855322	18.99741637	0.46

　先程も書いたように、地球と月との距離はおよそ 38 万 km、月の半径はおよそ 1700 km であり、比は 224 倍になります。そのため、地球から見た月の視直径の場合、初めに求めた近似的な表式を用いた場合も厳密な視直径の表式との誤差はごくわずかで、0.00034% にしかなりません。

　月から見た地球の視直径の場合は、地球の半径がおよそ 6400 km であることを考えると、比は小さくなって 59 倍となります。そのため、近似的な表式を用いた場合の誤差は大きくなりますが、それでも 0.0046% の違いでしかありません。地球-月系においては、月半径、地球半径ともに両者の距離より十分小さいため、近似的な表式でも十分正しい値を計算出来ると言えそうです。

　イオは木星の衛星のひとつで、比較的木星に近い位置を公転しています。イオの公転半径 (軌道長半径) は 421700 km、また木星半径は 69911 km なので、両者の比はおよそ 6 倍となります。この場合、近似的な表式を用いたことによる誤差は 0.46% となり、地球から見た月や、月から見た地球のケースよりずっと大きな値になることが分かります。それでも誤差は 1% 未満の値なので、イオから見た木星のケースでも誤差は微少であると言えます。

　もっと極端な場合も含めた、そのほかの計算例も示します。

$\displaystyle{\phi=2\arctan\left(\frac{r}{a\sqrt{1-\left(\frac{r}{a}\right)^{2}}}\right)}$ (度) $\displaystyle{\phi\approx\frac{2r}{a}}$ (度) 誤差 (%)

フォボスから見た火星 42.46140591 41.4963675 2.3

メティスから見た木星 66.21063253 62.5875819 5.5

静止衛星から見た地球 17.40097618 17.33417816 0.38

ISSから見た地球 140.4358626 108.8291369 23.3

	$\displaystyle{\phi=2\arctan\left(\frac{r}{a\sqrt{1-\left(\frac{r}{a}\right)^{2}}}\right)}$ (度)	$\displaystyle{\phi\approx\frac{2r}{a}}$ (度)	誤差 (%)
フォボスから見た火星	42.46140591	41.4963675	2.3
メティスから見た木星	66.21063253	62.5875819	5.5
静止衛星から見た地球	17.40097618	17.33417816	0.38
ISSから見た地球	140.4358626	108.8291369	23.3

　フォボスは、2 つある火星の衛星のうち火星に近い位置を公転している天体です。フォボスの軌道長半径は 9378 km、火星の赤道半径は 3396 km なので比は 3 倍も無い程度であり、誤差も大きくなる事が予想されますが、計算結果はやはり 2.3% と大きな値となりました。

　メティスは、発見されている木星の衛星の中で最も内側の軌道を公転しているものです。メティスの軌道長半径は 128000 km、木星の赤道半径は 69911 km なので比は 2 倍を切ります。計算すると、誤差は 5.5% になりました。

　下二段は、地球の周囲を回る人工衛星の軌道上から地球を見た場合に、地球の視直径が何度になるかを計算したものです。静止衛星は、赤道上空 35786 km の静止軌道を周回している人工衛星です。静止衛星の軌道長半径は、この値に地球の赤道半径を足した値になります。静止衛星から見た地球の視直径を計算すると、厳密な場合と近似した場合のどちらもおよそ 17 度となります。静止衛星の軌道長半径は地球半径よりも十分に大きいため、誤差は 0.38% に留まりました。

　一方、国際宇宙ステーション (International Space Station, ISS) の場合は上空およそ 400 km を周回しています。そのため、ISS の軌道長半径は 400 km に地球半径を足した値になりますが、地球の半径がおよそ 6400 km であるため ISS の軌道長半径は地球半径と大差ない値になります。そのため、厳密な式と近似式の誤差は 23.3% にもなります。

　従って、近似的な表式を用いて視直径を計算した場合、比較的惑星に近い位置を公転する衛星から惑星を見た場合では数% 程度の誤差が生じ得ることが分かります。逆に言えば、数% 程度の誤差は無視して考えていいようなおおまかな計算の場合は、近似的な式を用いても問題ないと言えます。また人工衛星の軌道上から地球を見た時は、特に低軌道では誤差が非常に大きく、近似的な表式は使えない事が分かります。

月・太陽の視直径と日食

　最も身近な天体である月と太陽の視直径と、日食との関連性について考えてみます。既に計算したように、地球から見た月の視直径と、地球から見た太陽の視直径は非常に近い値になるのでした。この一致は偶然の産物ですが、この非常に近い視直径が面白い現象を引き起こします。それは、日食の際の皆既日食 (total eclipse) と金環日食 (annular eclipse) の違いです。

　日食は、太陽-月-地球が一直線に並んで太陽が月に隠される現象です。月と太陽の見かけの大きさが非常に近いため、一直線になった時は太陽の大部分が隠されることになりますが、見かけの大きさの僅かな違いによって太陽が全て隠される場合 (皆既日食) と、全てを隠しきれずにリング状に見える場合 (金環日食) に分かれます。

　視直径は天体の大きさとその天体までの距離によって変わります。太陽と月の大きさは変化しないので、見かけの大きさが変わるとしたら天体までの距離が変化していることになります。先程の計算例では平均的な距離を使って計算しましたが、天体の軌道はわずかに円からずれた楕円形をしているため、距離は刻一刻と変化しています。

　例えば月の軌道離心率は 0.055 程度であり、月の軌道長半径 (平均的な距離) が 384400 km なのに対して、月が近地点 (最も地球に近付く点) にいる時は 363304 km、遠地点 (最も地球から遠ざかる点) にいる時は 405495 km と変化します。また地球の軌道離心率は 0.0167 程度であり、地球の軌道長半径がおよそ 1.496 × 10⁸ km なのに対して、地球が近日点 (最も太陽に近付く点) にいる時は 1.471 × 10⁸ km、遠日点 (最も太陽から遠ざかる点) にいる時は 1.521 × 10⁸ km と変化します。それぞれの具体的な数値は以下のようになります。

近点での視直径　平均視直径　遠点での視直径

地球から見た月 0.5479 度
(32.88 分) 0.5179 度
(31.07 分) 0.4909 度
(29.45 分)

地球から見た太陽 0.5422 度
(32.53 分) 0.5331 度
(31.99 分) 0.5244 度
(31.46 分)

	近点での視直径	平均視直径	遠点での視直径
地球から見た月	0.5479 度 (32.88 分)	0.5179 度 (31.07 分)	0.4909 度 (29.45 分)
地球から見た太陽	0.5422 度 (32.53 分)	0.5331 度 (31.99 分)	0.5244 度 (31.46 分)

　この結果から、視直径の大きさの順番は、

　近地点での月 > 近日点での太陽 > 遠日点での太陽 > 遠地点での月

であることが分かります。

　このように、月が軌道上のどの位置にいるか、また地球が軌道上のどの位置にいるかによって、月と太陽の見かけの大きさの大小は変化します。そのため、状況によっては「月の視直径 > 太陽の視直径」となって皆既日食になり、逆の「太陽の視直径 > 月の視直径」となった場合は金環日食になります。また、日食の最中にお互いの視直径の大きさが一致する特別な場合は、ある領域では皆既日食が見られ、それ以外の領域では金環日食になる場合があり、このような日食は金環皆既日食 (hybrid eclipse) と呼ばれます。その他、太陽-月-地球が一直線からややずれた場合は、太陽の一部分だけが隠される部分日食 (partial eclipse) となりますが、今回の視直径の話との関連性は薄いので省略します。

　天体の見かけの大きさの様々な例については、天体の見かけの大きさの具体例にまとめました。

参考文献

理科年表

2015年01月15日
2017年06月05日　更新

▼ページ更新履歴