ここでは、地球などの惑星の平衡温度を概算する方法を紹介します。
地球は太陽からのエネルギーを受けて温められています。
温められた結果どの程度の温度になるのかは、おおまかには太陽からどれくらいエネルギーを受け取っているかで決まります。
地球は太陽からエネルギーを受け取って温められますが、自らも温度に応じた熱輻射をしてエネルギーを失っています。
温度が釣り合っている状態というのは、太陽から受け取るエネルギーと地球が熱輻射で失うエネルギーが釣り合っているということです。
そこで、両者を比較する事を考えます。
地球軌道における、単位面積あたり、単位時間あたりの太陽放射エネルギーを太陽定数(Solar constant)と呼びます。
太陽定数は観測で測定することができ、最近の人工衛星を用いた観測によると、平均的には
まず、地球が受け取るエネルギーを考えます。
なお、反射率である「アルベド」には目的によって複数の種類があり、天体の温度を計算する際によく用いられるボンドアルベドは「入射する全エネルギーと反射する全エネルギーの比」を意味します。
次に地球が熱輻射で失うエネルギーを考えます。
したがって、地球のエネルギー収支は
エネルギー収支
太陽定数と太陽放射
太陽系惑星の平衡温度と表面温度
関連ページ
1層大気モデルを用いた大気の温室効果
2層大気モデルを用いた大気の温室効果
層大気モデルによる温室効果に関する考察
エネルギー収支
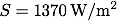 という値になります。
太陽活動は様々なタイムスケールで変動していて、それに伴ってエネルギーも変動するため、太陽定数は本当の意味での定数ではありません。
しかし、変動の大きさは0.1%程度の小さなものなので、一定と見なしても大きな間違いではありません。
という値になります。
太陽活動は様々なタイムスケールで変動していて、それに伴ってエネルギーも変動するため、太陽定数は本当の意味での定数ではありません。
しかし、変動の大きさは0.1%程度の小さなものなので、一定と見なしても大きな間違いではありません。
太陽からの放射を地球の断面積分で受け取ると考えます。
そうすると、単位時間に地球に降り注ぐエネルギーは、太陽定数と地球の断面積の積である
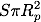 となります。
となります。
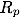 は地球の半径です。
しかし、地球は降り注ぐ太陽放射の全てを吸収出来るわけではなく、一部は反射してしまいます。
反射してしまった分の太陽放射は地球を温めるのには寄与しません。
天体の反射率はボンドアルベド(Bond Albedo)
は地球の半径です。
しかし、地球は降り注ぐ太陽放射の全てを吸収出来るわけではなく、一部は反射してしまいます。
反射してしまった分の太陽放射は地球を温めるのには寄与しません。
天体の反射率はボンドアルベド(Bond Albedo)
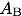 で表され、ボンドアルベドを用いると地球が受け取ることの出来るエネルギーは
で表され、ボンドアルベドを用いると地球が受け取ることの出来るエネルギーは
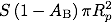 と書くことができます。
と書くことができます。
受け取るエネルギーと失うエネルギーが釣り合い、平衡状態になった時の温度を
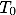 と置きます。
地球表面からは黒体輻射でエネルギーが失われると考えます。
温度Tの黒体から、単位時間・単位表面積あたり放射されるエネルギーは、ステファン・ボルツマンの法則より
と置きます。
地球表面からは黒体輻射でエネルギーが失われると考えます。
温度Tの黒体から、単位時間・単位表面積あたり放射されるエネルギーは、ステファン・ボルツマンの法則より
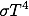 と表せます。
σはステファン・ボルツマン定数(Stefan-Boltzmann constant)です(シュテファン=ボルツマン定数、とも)。
地球の全表面が同じ温度であり全方向に等しく放射をすると仮定すると、地球全体から輻射で失われるエネルギーは、地球の表面積をかけて
と表せます。
σはステファン・ボルツマン定数(Stefan-Boltzmann constant)です(シュテファン=ボルツマン定数、とも)。
地球の全表面が同じ温度であり全方向に等しく放射をすると仮定すると、地球全体から輻射で失われるエネルギーは、地球の表面積をかけて
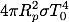 となります。
となります。
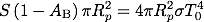
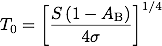
具体的に値を代入してみます。
地球のボンドアルベドはおよそ0.3であり、これと太陽定数、ステファン・ボルツマン定数を代入すると、地球の平衡温度は 255 Kとなります。
この値は摂氏に直すとおよそ-18℃になりますが、地球の現在の平均的な気温である15℃と比べるとかなり低い値となっています。
これは大気の効果を一切考慮していないためで、実際の地球では大気による温室効果が発生するために平衡温度よりも高い値を示します。
温室効果を厳密に考えるのは難しいですが、単純な大気モデルを用いて温室効果の大きさを評価する事は可能です。 これは別のページで紹介したいと思います。
なお、ここで求めた平衡温度は大気が全く存在しないという仮定を置いていますが、本当に大気が存在しなかった場合はアルベドの値も変わります。
アルベドを決めているのは惑星表面の組成や状態、大気などです。
特に氷や雲は反射率が高いためアルベドを大きくする効果がありますが、大気が存在しなければ雲も存在しません。
そのため、大気が無い場合に求めた平衡温度というのはあくまで理論上の存在であって、"地球から大気を取り去れば表面温度は-18℃になる"というわけではないことには注意が必要です。
上の計算では太陽定数を用いた計算を行いました。
太陽定数は地球軌道での太陽からのエネルギーフラックスを意味しています。
太陽全体から単位時間あたりに放射されるエネルギーは太陽光度(Solar luminosity)と呼ばれ、
太陽定数と太陽放射
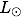 と表されます。
これを用いると、太陽定数は
と表されます。
これを用いると、太陽定数は
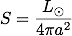
一方、太陽光度の方は、太陽が黒体輻射をしていると仮定すると次のように書くことができます。
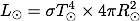
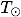 は太陽の有効温度、
は太陽の有効温度、
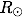 は太陽半径です。
これを用いると、太陽定数は次のように書くことができます。
は太陽半径です。
これを用いると、太陽定数は次のように書くことができます。
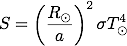
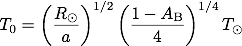
実際の値を代入すると(太陽半径:6.96×108 m、地球の軌道長半径:1.5×1011 m、太陽の有効温度:5778 K、ボンドアルベド:0.3)、平衡温度は 255 Kとなります。 当然ではありますが、太陽定数、ボンドアルベド、ステファン・ボルツマン定数を用いた計算結果と同じ結果になります。 こちらの式の場合は、太陽定数、ステファン・ボルツマン定数の値を知らなくても使えます。
なお、この式は地球に限らず一般的に使用することができます。 軌道長半径には任意の天体の軌道長半径、ボンドアルベドにその天体の数値を代入すれば、任意の天体の平衡温度の計算が出来ます。 さらに、太陽半径と太陽の有効温度を別の恒星の値を代入すれば、任意の恒星の周りを公転する天体の平衡温度を計算することができます。
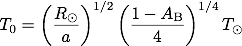
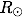 、a、
、a、
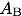 、
、
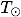 はそれぞれ太陽半径、天体の軌道長半径、天体のボンドアルベド、太陽の有効温度である。
はそれぞれ太陽半径、天体の軌道長半径、天体のボンドアルベド、太陽の有効温度である。
太陽系惑星の平衡温度と表面温度
上で求めた式から、太陽系内の天体の平衡温度を計算出来ます。
太陽系の惑星の平衡温度を、それぞれの軌道長半径とボンドアルベドを代入して計算すると、次のグラフのようになります。
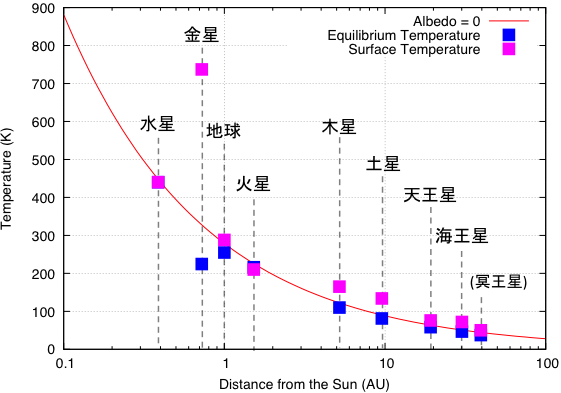
平衡温度の式を見ると分かるように、アルベドの違いは1/4乗でしか効いてこないため、各惑星の平衡温度はアルベド=0の赤い線を僅かに下回る程度となります。 例外は金星で、金星は反射率の高い雲で全面が覆われているためアルベドが他の惑星に比べて遥かに大きな値となるため、アルベド=0の赤い線を大きく下回る平衡温度となります。 太陽に近いにも関わらず地球すら下回り、火星と同じ程度です。
一方実際の惑星の表面温度は、平衡温度よりも高くなります。 地球も青い点より紫の点の方が高くなっています。 木星や土星は特に違いが大きくなっていますが、これは木星や土星といった巨大ガス惑星は、収縮することによって重力エネルギーを熱の形で解放する「ケルビン・ヘルムホルツ機構(Kelvin-Helmholtz mechanism)」がはたらくことによって内部からの熱の供給があるためです。 木星も土星も、太陽から受け取るエネルギーと同等か上回る程度の熱を内部から供給しています。
ここでも金星は例外で、平衡温度から遥かにかけ離れた表面温度になっています。 金星は大量の大気を保持していて、その大気による強力な温室効果がはたらくことによって表面温度が高温になります。
このグラフから、太陽との距離が 0.1 AUを下回るような非常に近い場所にいる天体は、表面温度が1000 Kを超えることが分かります。
太陽系内にはそのような天体はありませんが(一時的に飛来する彗星や小惑星を除く)、太陽系外惑星では 0.05 AU程度の非常に近い位置を公転する惑星があることが分かっていて、表面温度は 1000 Kを超えます。
恒星から非常に近い所、目安としては 0.05 AU程度を公転している巨大ガス惑星は「ホットジュピター(hot Jupiter)」と呼ばれ、それよりサイズが一回り小さいものは「ホットネプチューン(hot Neptune)」と呼ばれます。
ただしこれらは明確な定義があるわけではありません。
参考文献
惑星などの天体に関する物理量・理科年表 (丸善)
・Planetary fact sheets (NSSDC/NASA)