ポリトロープ球とレーン=エムデン方程式のページでは、密度と圧力のポリトロープ関係を仮定して、天体の内部構造を記述する式であるレーン=エムデン方程式 (Lane-Emden equation)を導出しました。
一般にはレーン=エムデン方程式を解析的に解くのは難しく、数値計算をする必要がありますが、いくつかの場合においては解析解があることが知られています。
ここでは、レーン=エムデン方程式の解析解について紹介します。
目次:
関連ページ:
レーン=エムデン方程式
まずはもう一度レーン=エムデン方程式を書いておきます。
天体の内部構造を記述するレーン=エムデン方程式は、以下のように書き表される。 \begin{align*} \frac{1}{\xi^{2}}\frac{d}{d\xi}\left(\xi^{2}\frac{d\theta}{d\xi}\right)=-\theta^{N} \end{align*} ここで、\(\theta\) は無次元化した密度 \(\rho=\rhoc\theta^{N}\) である。 また、\(\xi\)は無次元化した半径 \(\displaystyle{\xi=\frac{r}{\alpha}}\)、 \(\displaystyle{\alpha^{2}=\frac{\left(N+1\right)\pc}{4\pi G\rhoc^{2}}}\) である。 添字の "c" は中心での値を意味する。 また、\(N\) はポリトロープ関係のポリトロープ指数である。
中心での境界条件は、\(\xi=0\) のとき \(\theta=1\)、 \(\displaystyle{\frac{d\theta}{d\xi}=0}\) である。
この式を一般の \(N\) に対して解析的に解くことは出来ませんが、ある特定の \(N\) にの場合は解析的に解くことが可能です。 その時の解はそれぞれ、
(i) \(N=0\) のとき \begin{align*} \theta\left(\xi\right)=1-\frac{1}{6}\xi^{2} \end{align*}
(ii) \(N=1\) のとき \begin{align*} \theta\left(\xi\right)=\frac{\sin\xi}{\xi} \end{align*}
(iii) \(N=5\) のとき \begin{align*} \theta\left(\xi\right)=\frac{1}{\sqrt{1+\frac{1}{3}\xi^{2}}} \end{align*}
となることが知られています。
ここでは、これらの解析解の導出を紹介します。
まずは最も簡単な状況である、\(N=0\) の時の解析解の導出方法です。
レーン=エムデン方程式に \(N=0\) を代入すると、以下のようになります。
\begin{align*}
\frac{1}{\xi^{2}}\frac{d}{d\xi}\left(\xi^{2}\frac{d\theta}{d\xi}\right)=-1
\end{align*}
両辺に \(\xi^{2}\) をかけて
\begin{align*}
\frac{d}{d\xi}\left(\xi^{2}\frac{d\theta}{d\xi}\right)=-\xi^{2}
\end{align*}
とします。
この式の両辺を積分すると、
\begin{align*}
\xi^{2}\frac{d\theta}{d\xi}=-\frac{1}{3}\xi^{3}+C_{1}
\end{align*}
となります。
\(C_{1}\) は積分定数です。
両辺を \(\xi^{2}\) で割るとこの式は
\begin{align*}
\frac{d\theta}{d\xi}=-\frac{1}{3}\xi+\frac{C_{1}}{\xi^{2}}
\end{align*}
となり、再び積分すれば
\begin{align*}
\theta\left(\xi\right)=-\frac{1}{6}\xi^{2}-\frac{C_{1}}{\xi^{2}}+C_{2}
\end{align*}
となります。
\(C_{2}\) は同じく積分定数です。
これは \(N=0\) の時の方程式の一般解になっています。
次に境界条件から積分定数を決定して行きます。
まず、\(\xi=0\) の時に \(\displaystyle{\frac{d\theta}{d\xi}=0}\) であるという境界条件を考えます。
\(\xi\rightarrow0\) の極限を考えると、\(C_{1}\) が 0 でない値を持っている場合は分母が 0 に近付くため無限大に発散してしまいます。
そのため、境界条件を満たす為には \(C_{1}=0\) である必要があります。
次に、\(\xi=0\) の時に \(\theta=1\) という条件を満たす為には、\(C_{2}=1\) とすれば良いことが分かります。
従って、\(N=0\) の時のレーン=エムデン方程式の解析解は以下のようになります。
\begin{align*}
\theta\left(\xi\right)=1-\frac{1}{6}\xi^{2}
\end{align*}
次に、\(N=1\) の場合を考えます。
レーン=エムデン方程式に \(N=1\) を代入すると、次の方程式が得られます。
\begin{align*}
\frac{1}{\xi^{2}}\frac{d}{d\xi}\left(\xi^{2}\frac{d\theta}{d\xi}\right)+\theta=0
\end{align*}
先程の \(N=0\) の時は \(\theta\) は一つだけだったので積分は簡単でしたが、この場合は 2 つ入っていてこのまま積分することができません。
そのため、変数変換をして積分出来る形にしてやります。
ここで、
\begin{align*}
z=\xi\theta
\end{align*}
という新しい変数 \(z\) を導入します。
この関係式を用いると、
\begin{align*}
\frac{d\theta}{d\xi}=\frac{d}{d\xi}\left(\frac{z}{\xi}\right)=\frac{1}{\xi}\frac{dz}{d\xi}-\frac{z}{\xi^{2}}
\end{align*}
であることが分かります。
両辺に \(\xi\) をかけると
\begin{align*}
\xi^{2}\frac{d\theta}{d\xi}=\xi\frac{dz}{d\xi}-z
\end{align*}
となり、これを \(\xi\) で微分すると
\begin{align*}
\frac{d}{d\xi}\left(\xi^{2}\frac{d\theta}{d\xi}\right)=\frac{d}{d\xi}\left(\xi\frac{dz}{d\xi}-z\right)=\xi\frac{d^{2}z}{d\xi^{2}}
\end{align*}
が得られます。
よって、元の式に代入して元の式から \(\theta\) を消去して \(z\) に置き換えた方程式は次のようになります。
\begin{align*}
\frac{d^{2}z}{d\xi^{2}}+z=0
\end{align*}
非常にシンプルな 2 階微分方程式に持って行くことができました。
この微分方程式は、\(z\) を 2 階微分すると再び \(z\) に戻る (しかし符号は変わる) という形になっています。
このような形の微分方程式の一般解は良く知られており、次のような形で表されます。
\begin{align*}
z=A\cos\xi+B\sin\xi
\end{align*}
ただし、\(A\) と \(B\) はそれぞれ任意の定数 (積分定数) です。
変数を元に戻すと、
\begin{align*}
\theta\left(\xi\right)=\frac{A\cos\xi}{\xi}+\frac{B\sin\xi}{\xi}
\end{align*}
という形になります。
これは、\(N=1\) の時の方程式の一般解になっています。
先程と同様に、境界条件から定数を決定して行きます。
\(\xi\rightarrow0\) の時 \(\theta\rightarrow1\) であるという条件を考えます。
この時、\(A\) が値を持つ場合は右辺の第一項は発散してしまうため、\(A=0\) である必要があります。
また右辺第二項については、
\begin{align*}
\lim_{\xi\rightarrow0}\frac{\sin\xi}{\xi}=1
\end{align*}
となることから、\(B=1\) である必要があります。
従って、\(N=1\) の時のレーン=エムデン方程式の解析解は以下のようになります。
\begin{align*}
\theta\left(\xi\right)=\frac{\sin\xi}{\xi}
\end{align*}
一つ目の境界条件だけで係数が 2 つとも決まってしまいましたが、念のためもう一つの境界条件を満たしているかどうかも確認しておきます。
もう一つの境界条件を満たすためには、\(\xi\rightarrow0\) の時に \(\displaystyle{\frac{d\theta}{d\xi}\rightarrow0}\) となっている必要があります。
\(\theta\) を \(\xi\) で微分すると
\begin{align*}
\frac{d\theta}{d\xi}=\frac{\xi\cos\xi-\sin\xi}{\xi^{2}}
\end{align*}
となるので、これの \(\xi\rightarrow0\) の極限が 0 になるかを確認すれば良いということになります。
これを計算すると、
\begin{align*}
\lim_{\xi\rightarrow0}\frac{d\theta}{d\xi}&=\lim_{\xi\rightarrow0}\frac{\xi\cos\xi-\sin\xi}{\xi^{2}}\\
&=-\lim_{\xi\rightarrow0}\frac{\xi\sin\xi}{2\xi}\\
&=-\frac{1}{2}\lim_{\xi\rightarrow0}\sin\xi\\
&=0
\end{align*}
となり、境界条件が満たされていることが確認出来ました。
最初の形は分母も分子も 0 になってしまうため不定形ですが、1 行目から 2 行目に移るときに「ロピタルの定理」を用いています。
\(N=1\) を代入して得られる方程式
\begin{align*}
\frac{1}{\xi^{2}}\frac{d}{d\xi}\left(\xi^{2}\frac{d\theta}{d\xi}\right)+\theta=0
\end{align*}
は、球ベッセル関数
\begin{align*}
\frac{d}{dr}\left(r^{2}\frac{dR}{dr}\right)+\left[k^{2}r^{2}-n\left(n+1\right)\right]=0
\end{align*}
において、\(k=1\)、\(n=0\) の場合の形状をしています。
この時の解は、\(A\) と \(B\) を定数として、
\begin{align*}
\theta\left(\xi\right)=Aj_{0}\!\left(\xi\right)+Bn_{0}\!\left(\xi\right)
\end{align*}
という形で表されます。
ここで
\begin{align*}
j_{n}\!\left(z\right)=\left(-1\right)^{n}\left(\frac{d}{dz}\right)^{n}\frac{\sin z}{z}
\end{align*}
であり、\(n=0\) の場合は
\begin{align*}
j_{0}\!\left(z\right)=\frac{\sin z}{z}
\end{align*}
となります。
同様に、
\begin{align*}
n_{0}\!\left(z\right)=\frac{-\cos z}{z}
\end{align*}
であることが知られています。
よって、これらの結果から一般解が求められ、同様に境界条件を課すことで定数が決定でき、最終的に
\begin{align*}
\theta\left(\xi\right)=\frac{\sin\xi}{\xi}
\end{align*}
という解が得られます。
別解と書きましたが、おそらく歴史的な経緯としては、\(N=1\) の時のレーン=エムデン方程式が球ベッセル関数の形をしていることから解が導かれたのではないかと思われます。
最初に紹介した変数変換を用いた解析解の導出も、初めから解の形を知っているとすんなりと導入出来る変数変換です。
最後に、\(N=5\) の場合を考えます。
レーン=エムデン方程式に \(N=5\) を代入すると、次の方程式が得られます。
\begin{align*}
\frac{1}{\xi^{2}}\frac{d}{d\xi}\left(\xi^{2}\frac{d\theta}{d\xi}\right)=-\theta^{5}
\end{align*}
この式を解くのは非常に困難ですが、特殊な変数変換を行うことで解ける形へ持って行くことが可能です。
ここでは無次元化した半径 \(\xi\) と、無次元化した密度の \(\theta\) の両方を、以下のように変数変換します。
これらの変数変換の関係式から、
\begin{align*}
\frac{d\xi}{dt}=-\xi
\end{align*}
となることが分かります。
また、\(Z\) の \(\xi\) 微分は
\begin{align*}
\frac{dZ}{d\xi}=\frac{dZ}{dt}\frac{dt}{d\xi}=-\frac{1}{\xi}\frac{dZ}{dt}
\end{align*}
となるため、微分演算子には
\begin{align*}
\frac{d}{d\xi}=-\frac{1}{\xi}\frac{d}{dt}
\end{align*}
という関係があることも分かります。
これらの関係を用いて、\(N=5\) の時のレーン=エムデン方程式を変形し、\(Z\) と \(t\) の式に書き換えていきます。
まず、\(\theta=\left(2\xi\right)^{-\frac{1}{2}}Z\) より、\(\theta\) の \(\xi\) 微分は
\begin{align*}
\frac{d\theta}{d\xi}&=-\frac{1}{2\sqrt{2}}\xi^{-\frac{3}{2}}Z+\frac{1}{\sqrt{2}}\xi^{-\frac{1}{2}}\frac{dZ}{d\xi}\\
&=-\frac{1}{2\sqrt{2}}\xi^{-\frac{3}{2}}Z-\frac{1}{\sqrt{2}}\xi^{-\frac{3}{2}}\frac{dZ}{dt}
\end{align*}
となります。
両辺に \(\xi^{2}\) をかけると
\begin{align*}
\xi^{2}\frac{d\theta}{d\xi}=-\frac{1}{2\sqrt{2}}\xi^{\frac{1}{2}}-\frac{1}{\sqrt{2}}\xi^{\frac{1}{2}}\frac{dZ}{dt}
\end{align*}
となります。
これを \(\xi\) で微分した式を考えると、次のように計算出来ます。
\begin{align*}
\frac{d}{d\xi}\left(\xi^{2}\frac{d\theta}{d\xi}\right)&=-\frac{1}{4\sqrt{2}}\xi^{-\frac{1}{2}}Z-\frac{1}{2\sqrt{2}}\xi^{\frac{1}{2}}\frac{dZ}{dt}-\frac{1}{2\sqrt{2}}\xi^{-\frac{1}{2}}\frac{dZ}{dt}-\frac{1}{\sqrt{2}}\xi^{\frac{1}{2}}\frac{d}{d\xi}\left(\frac{dZ}{dt}\right)\\
&=-\frac{1}{4\sqrt{2}}\xi^{-\frac{1}{2}}Z+\frac{1}{\sqrt{2}}\xi^{-\frac{1}{2}}\frac{d^{2}Z}{dt^{2}}
\end{align*}
ここで、
\begin{align*}
-\xi^{2}\theta^{5}=-\xi^{2}\frac{1}{4\sqrt{2}}\xi^{-\frac{5}{2}}Z^{5}=-\frac{1}{4\sqrt{2}}\xi^{-\frac{1}{2}}Z^{5}
\end{align*}
となるので、元のレーン=エムデン方程式は
\begin{align}
\frac{d^{2}Z}{dt^{2}}=\frac{1}{4}Z\left(1-Z^{4}\right)
\tag{A}
\label{eqa}
\end{align}
という形に書き直すことができます。
これで、方程式を \(Z\) と \(t\) のみの微分方程式に変形することができました。
この 2 階微分方程式を、まず 1 回積分します。
式 \eqref{eqa} の両辺に \(\displaystyle{\frac{dZ}{dt}}\) をかけると、式は以下のようになります。
\begin{align}
\left(\frac{dZ}{dr}\right)\left(\frac{d^{2}Z}{dt^{2}}\right)=\frac{1}{4}Z\left(\frac{dZ}{dt}\right)-\frac{1}{4}Z^{5}\left(\frac{dZ}{dr}\right)
\tag{A'}
\label{eqap}
\end{align}
この式の左辺は \(Z\) の 2 階微分に \(Z\) の 1 階微分がかかった形になっており、次のように変形出来ます。
\begin{align*}
\left(\frac{dZ}{dr}\right)\left(\frac{d^{2}Z}{dt^{2}}\right)=\frac{1}{2}\frac{d}{dt}\left[\left(\frac{dZ}{dt}\right)^{2}\right]
\end{align*}
微分を実行してみると、左辺の形になることは容易に確かめられます。
また、右辺も
\begin{align*}
Z\left(\frac{dZ}{dt}\right)=\frac{1}{2}\frac{d}{dt}\left(Z^{2}\right)
\end{align*}
などと変形出来ることを用いると、式 \eqref{eqap} を積分した結果は次のようになります。
\begin{align*}
\frac{1}{2}\left(\frac{dZ}{dt}\right)^{2}=\frac{1}{8}Z^{2}-\frac{1}{24}Z^{6}+D
\end{align*}
ここで、\(D\) は積分定数です。
この段階で、境界条件から \(D\) を決めておきます。
変数変換の式 \(Z=\left(2\xi\right)^{\frac{1}{2}}\theta\) より、\(\xi=0\) の時は \(Z=0\) になることが分かります。
ここで、\(\displaystyle{\frac{dZ}{dt}}\) を \(\xi\) や \(\theta\) を用いて表すと、次のようになります。
\begin{align*}
\frac{dZ}{dt}&=\frac{dZ}{d\xi}\frac{d\xi}{dt}\\
&=\frac{d\xi}{dt}\frac{d}{d\xi}\left(\left(2\xi\right)^{\frac{1}{2}}\theta\right)\\
&=\xi\left(\frac{\sqrt{2}}{2}\xi^{-\frac{1}{2}}\theta+\sqrt{2}\xi^{\frac{1}{2}}\frac{d\theta}{d\xi}\right)\\
&=-\sqrt{2}\left(\frac{1}{2}\xi^{\frac{1}{2}}\theta+\xi^{\frac{3}{2}}\frac{d\theta}{d\xi}\right)
\end{align*}
従って、\(\xi=0\) の時は \(\displaystyle{\frac{dZ}{dt}}\) も 0 となることが分かります。
この条件を満たすためには、\(D=0\) である必要があります。
よって、\(D=0\) を代入して整理した結果、次のような式が得られます。
\begin{align*}
\frac{dZ}{Z\left(1-\frac{1}{3}Z^{4}\right)^{\frac{1}{2}}}=\pm\frac{1}{2}dt
\end{align*}
正負の二通りがありますが、ここで物理的に意味がある解が得られるのは負の符号を選んだ時です (詳細はこちら)。
従って、ここで解くべき微分方程式は次の方程式です。
\begin{align}
\frac{dZ}{Z\left(1-\frac{1}{3}Z^{4}\right)^{\frac{1}{2}}}=-\frac{1}{2}dt
\tag{B}
\label{eqb}
\end{align}
この方程式を解くために、さらに次のような変数変換を行います。
\begin{align*}
\frac{1}{3}Z^{4}=\sin^{2}\phi
\end{align*}
この式の微分形は以下のようになります。
\begin{align*}
\frac{4}{3}Z^{3}dZ=2\sin\phi\cos\phi\,d\phi
\end{align*}
これらを用いて、式 \eqref{eqb} を書き換えて行きます。
式 \eqref{eqb} の左辺は、変数変換の式を代入して整理すると次のようになります。
\begin{align*}
\frac{dZ}{Z\left(1-\frac{1}{3}Z^{4}\right)^{\frac{1}{2}}}
&=\frac{1}{Z\left(1-\sin^{2}\phi\right)^{\frac{1}{2}}}\frac{3}{4Z^{3}}2\sin\phi\cos\phi\,d\phi\\
&=\frac{3}{2}\frac{1}{Z^{4}}\frac{\sin\phi\cos\phi\,d\phi}{\left(1-\sin^{2}\phi\right)^{\frac{1}{2}}}\\
&=\frac{1}{2\sin^{2}\phi}\frac{\sin\phi\cos\phi}{\cos\phi}d\phi\\
&=\frac{1}{2}\frac{1}{\sin\phi}d\phi\\
&=\frac{1}{2}\cosec\phi
\end{align*}
"\(\cosec\)" は三角関数の一種で、「コセカント (余割)」です。
式を見ると分かるように、\(\sin\) の逆数となっています。
省略して "\(\csc\)" と表記されることもあります。
よって、式 \eqref{eqb} は以下の微分方程式へと変形出来ます。
\begin{align*}
\cosec\phi\,d\phi=-dt
\end{align*}
両辺を積分すると、
\begin{align*}
\ln\abs{\tan\frac{\phi}{2}}=-t+C^{\prime}
\end{align*}
となります。
\(C^{\prime}\) は積分定数です。
左辺の \(\cosec\) の積分については後ほど紹介します。
対数を外すと、式は
\begin{align*}
\tan\frac{\phi}{2}=Ce^{-t}
\tag{C}
\label{eqc}
\end{align*}
となります。
\(C\) は同様に積分定数ですが、上式の対数を外してまとめた結果に出てくる \(C^{\prime}\) を含む定数部分を \(C\) と置き直しています。
これで、方程式自体は積分することができました。
ここから、元の変数へと直していきます。
ここで行った変数変換は
\begin{align*}
\frac{1}{3}Z^{4}=\sin^{2}\phi
\end{align*}
というものでした。
これを上手く変形してやると、
\begin{align*}
Z^{4}&=3\sin^{2}\phi\\
&=\frac{12\tan^{2}\frac{\phi}{2}}{\left(1+\tan^{2}\frac{\phi}{2}\right)^{2}}
\end{align*}
となります (この変形についても後ほど紹介します)。
こう変形すると式 \eqref{eqc} をそのまま代入することができ、結果は
\begin{align*}
Z^{4}=\frac{12C^{2}e^{-2t}}{\left(1+C^{2}e^{-2t}\right)^{2}}
\end{align*}
となります。
よって、両辺の 4 乗根をとると、\(Z\) は以下のように表すことができます。
\begin{align*}
Z=\pm\left[\frac{12C^{2}e^{-2t}}{\left(1+C^{2}e^{-2t}\right)^{2}}\right]^{\frac{1}{4}}
\end{align*}
\(Z\) は \(Z=\left(2\xi\right)^{\frac{1}{2}}\theta\) という変数変換をしたものなので、物理的に意味があるのは \(Z\) が正の場合のみです。
よって、ここでは正の場合のみを解として採用すれば良いことが分かります。
さらに \(\displaystyle{\theta=\left(\frac{1}{2}e^{t}\right)^{\frac{1}{2}}Z}\) や \(\xi=e^{-t}\) を用いて \(\theta\) の式に直すと、
\begin{align*}
\theta=\left[\frac{3C^{2}}{\left(1+C^{2}e^{-2t}\right)^{2}}\right]^{\frac{1}{4}}=\left[\frac{3C^{2}}{\left(1+C^{2}\xi^{2}\right)^{2}}\right]^{\frac{1}{4}}
\end{align*}
となり、ようやく最初の変数である \(\xi\) と \(\theta\) の式にまで戻ってくることができました。
ここで境界条件から積分定数を決定します。
\(\xi=0\) で \(\theta=1\) という条件より、
\begin{align*}
1=\left(3C^{2}\right)^{\frac{1}{4}}
\end{align*}
となり、
\begin{align*}
C^{2}=\frac{1}{3}
\end{align*}
が得られます。
よって積分定数を代入すると
\begin{align*}
\theta=\left[\frac{1}{\left(1+\frac{1}{3}\xi^{2}\right)^{2}}\right]^{\frac{1}{4}}=\frac{1}{\left(1+\frac{1}{3}\xi^{2}\right)^{\frac{1}{2}}}
\end{align*}
となります。
従って、\(N=5\) の時のレーン=エムデン方程式の解析解は以下のようになります。
\begin{align*}
\theta\left(\xi\right)=\frac{1}{\sqrt{1+\frac{1}{3}\xi^{2}}}
\end{align*}
\(N=0\) や \(N=1\) の場合と比べると、遥かに煩雑な計算が必要であることが分かります。
上で出て来た、\(\cosec\) の不定積分を紹介します。
\(\cosec\) は \(\sin\) の逆数なので、次のように式変形出来ます。
\begin{align*}
\int\cosec\,x\,dx=\int\frac{1}{\sin x}dx
\end{align*}
右辺を次のように変形して行きます。
\begin{align*}
\int\cosec\,x\,dx&=\int\frac{1}{\sin x}dx\\
&=\int\frac{\sin x}{\sin^{2}x}dx\\
&=\int\frac{\sin x}{1-\cos^{2}x}dx
\end{align*}
ここで、
\begin{align*}
t=\cos x
\end{align*}
と変数変換します。
微分をとると
\begin{align*}
dt=-\sin x\,dx
\end{align*}
となります。
これを使って式を書き換えると、
\begin{align*}
\int\cosec\,x\,dx&=\int\frac{-dt}{1-t^{2}}\\
&=\frac{-dt}{\left(1-t\right)\left(1+t\right)}
\end{align*}
となります。
部分分数分解を用いて式を書き換えると
\begin{align*}
\int\frac{-dt}{\left(1-t\right)\left(1+t\right)}=-\frac{1}{2}\int\left(\frac{1}{1-t}+\frac{1}{1+t}\right)dt
\end{align*}
となり、簡単に積分出来る形に変形出来ます。
積分を実行すると、
\begin{align*}
-\frac{1}{2}\int\left(1-t\right)\left(1+t\right)dt&=-\frac{1}{2}\left(\ln\abs{1-t}+\ln\abs{1+t}+C^{\prime}\right)\\
&=-\frac{1}{2}\ln\abs{\frac{1+t}{1-t}}+C\\
&=\frac{1}{2}\ln\abs{\frac{1-t}{1+t}}+C
\end{align*}
となります。
\(C\) は積分定数です。
ここで \(t=\cos x\) であることから、絶対値の中は常に 0 以上の値を取ることが分かるため、絶対値を外して書くことができます。
また、
\begin{align*}
\ln\left(\frac{1-t}{1+t}\right)&=\ln\left(\frac{1-\cos x}{1+\cos x}\right)\\
&=\ln\left(\frac{\sin^{2}\frac{x}{2}}{\cos^{2}\frac{x}{2}}\right)\\
&=\ln\left(\tan^{2}\frac{x}{2}\right)
\end{align*}
となるので、積分は
\begin{align*}
\int\cosec\,x\,dx&=\frac{1}{2}\ln\left(\tan^{2}\frac{x}{2}\right)+C\\
&=\ln\left(\tan^{2}\frac{x}{2}\right)^{\frac{1}{2}}+C\\
&=\ln\abs{\tan\frac{x}{2}}+C
\end{align*}
となります。
よって、\(\cosec\) の不定積分は以下のような形になることが分かりました。
\begin{align*}
\int\cosec\,x\,dx=\int\frac{1}{\sin x}dx=\ln\abs{\tan\frac{x}{2}}+C
\end{align*}
計算の途中で、以下のような変形を用いました。
\begin{align*}
Z^{4}&=3\sin^{2}\phi\\
&=\frac{12\tan^{2}\frac{\phi}{2}}{\left(1+\tan^{2}\frac{\phi}{2}\right)^{2}}
\end{align*}を
計算して出て来た結果に \(\displaystyle{\tan\frac{\phi}{2}=Ce^{-t}}\) という項が出てくるため、\(\displaystyle{\tan\frac{\phi}{2}}\) をそのまま代入出来るようにひねり出したものです。
これの途中計算を書いておきます。
\(\sin^{2}\phi\) は、以下のように変形出来ます。
\begin{align*}
\sin^{2}\phi&=1-\cos^{2}\phi\\
&=\left(1-\cos\phi\right)\left(1+\cos\phi\right)\\
&=\frac{1-\cos\phi}{1+\cos\phi}\left(1+\cos\phi\right)^{2}\\
&=\tan^{2}\frac{\phi}{2}\left(1+\cos\phi\right)^{2}
\end{align*}
最後の式変形の所で \(\tan\) の半角の公式を用いています。
次に、後ろの項を以下のように変形して行きます。
\begin{align*}
\left(1+\cos\phi\right)^{2}&=\left(\frac{1}{1+\cos\phi}\right)^{-2}\\
&=\left[\frac{\frac{1}{2}\left(1+\cos\phi+1-\cos\phi\right)}{1+\cos\phi}\right]^{-2}\\
&=4\left[1+\frac{1-\cos\phi}{1+\cos\phi}\right]^{-2}\\
&=4\left(1+\tan^{2}\frac{\phi}{2}\right)^{-2}
\end{align*}
従って、
計算途中の
\begin{align*}
\frac{dZ}{Z\left(1-\frac{1}{3}Z^{4}\right)^{\frac{1}{2}}}=\pm\frac{1}{2}dt
\end{align*}
の部分で、物理的に意味があるのは負の符号を選んだ時であるとして負符号のときのみを選び、最終的な解を導出しました。
ここでは、正符号の場合の解を導出して、物理的に意味の無い解になることを確認します。
正負両方を残したまま計算を進めると、解くべき微分方程式は次のようになります。
\begin{align*}
\cosec\,\phi\,d\phi=\pm dt
\end{align*}
これを積分すると次のようになります。
\begin{align*}
\tan\frac{\phi}{2}=Ce^{\pm t}
\end{align*}
ここで、負の符号である
\begin{align*}
\tan\frac{\phi}{2}=Ce^{-t}
\end{align*}
を選んだ場合が、上で紹介した計算でした。
一方、正の符号を選んだ場合、つまり
\begin{align*}
\tan\frac{\phi}{2}=Ce^{t}
\end{align*}
を選んだ場合は、\(\displaystyle{\frac{1}{3}Z^{4}=\sin^{2}\phi}\) より、計算は以下のようになります。
\begin{align*}
Z^{4}=\frac{12\tan^{2}\frac{\phi}{2}}{\left(1+\tan^{2}\frac{\phi}{2}\right)^{2}}=\frac{12C^{2}e^{2t}}{\left(1+C^{2}e^{2t}\right)^{2}}
\end{align*}
よって 4 乗根をとると
\begin{align*}
Z=\pm\left[\frac{12C^{2}e^{2t}}{\left(1+C^{2}e^{2t}\right)^{2}}\right]^{\frac{1}{4}}
\end{align*}
になります。
同様に正の方のみを選択します。
\(\theta\) の式に直すと、
\begin{align*}
\theta=\left[\frac{3C^{2}e^{4t}}{\left(1+C^{2}e^{2t}\right)^{2}}\right]^{\frac{1}{4}}
\end{align*}
ここで \(\xi=e^{-t}\) を用いて \(t\) を \(\xi\) に置き換えると、
\begin{align*}
\theta=\left[\frac{3C^{2}}{\left(\xi^{8}+C^{2}\xi^{6}\right)^{2}}\right]^{\frac{1}{4}}
\end{align*}
となります。
ここで境界条件を考えてみます。
\(C\) が値を持つ時、\(\xi\rightarrow0\) を考えると \(\theta\) は無限大に発散してしまいます。
無限大に発散しない為には \(C=0\) 以外に選択肢はありませんが、そうすると \(\xi\) の値に関わらず \(\theta=0\) となってしまいます。
つまり、境界条件を満たす解は存在しないということになります。
\(N=0\) の時の解析解
\(N=1\) の時の解析解
別解
\(N=5\) の時の解析解
付録
\(\cosec\) の不定積分
\(\sin^{2}\phi\) の変形
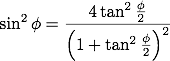
正負の選び方
参考文献
高原文郎「宇宙物理学」(朝倉書店)
Lane-Emden Differential Equation -- from Wolfram MathWorld
Chandrasekhar, S. "An Introduction to the Study of Stellar Structure" (Dover)
2015年11月18日
2017年06月05日 更新