地表・大気の熱輻射を全て吸収する場合

　計算結果の検算も兼ねて、まずは簡単なモデルから始めます。 太陽からの放射は 2 つの大気層で同じ吸収率で吸収され、地表からの熱輻射は全て大気層に吸収され、また大気層からの熱輻射も別の大気層に全て吸収されるという状況を考えます。 考えるのは以下の状況です。

　地表の温度は \(\Te\)、2 つの大気層のうち下層を大気層 1、上層を大気層 2 とし、それぞれ温度を \(T_{1}\)、\(T_{2}\) とします。 それぞれの輻射は \(\Ie=\sigma\Te^{4}\)、\(I_{1}=\sigma T_{1}^{4}\)、\(I_{2}=\sigma T_{2}^{4}\) とします。 この状況の模式図は下図のようになります。

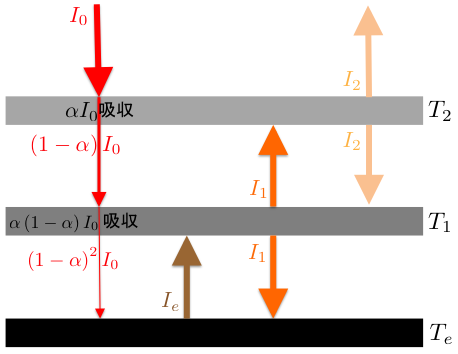
　まず地表のエネルギー収支を考えます。 太陽からの放射 \(I_{0}\) は、 大気層 2 を通過した後は \(\left(1-\alpha\right)I_{0}\) となり、さらに大気層 1 を通過した後は \(\left(1-\alpha\right)^{2}I_{0}\) となります。 これが太陽から受け取るエネルギーになります。 大気層 2 からの輻射は全て大気層 1 に吸収されると仮定しているため、地表には到達しません。 大気層 1 からの輻射は全て吸収します。 そして \(\Ie\) の放射をしていることになるため、地表のエネルギー収支は以下のようになります。 \begin{align*} \left(1-\alpha\right)^{2}I_{0}+I_{1}=\Ie \end{align*}

　次に大気層 1 のエネルギー収支を考えます。 大気層 2 を通過して大気層 1 まで届く太陽放射は \(\left(1-\alpha\right)I_{0}\) であり、これに \(\alpha\) をかけた分が大気層 1 が吸収する放射です。 また、地表からの輻射は全て吸収し、大気層 2 からの輻射も全て吸収します。 そして上下に輻射をしているため、大気層 1 のエネルギー収支は以下のようになります。 \begin{align*} \alpha\left(1-\alpha\right)I_{0}+\Ie+I_{2}=2I_{1} \end{align*}

　大気層 2 は、太陽からの放射のうち \(\alpha\) をかけた分を吸収し、大気層 1 からの輻射は全て吸収します。 地表からの輻射は大気層 1 に全て吸収されるため到達しません。 そして上下に輻射をしているため、大気層 2 のエネルギー収支は次のように書けます。 \begin{align*} \alpha I_{0}+I_{1}=2I_{2} \end{align*}

　次に、地表からの熱輻射と大気層からの熱輻射が宇宙空間に"漏れ出す"ような、より一般的な状況を考えます。 以下のような状況を考えます。

　模式図は以下のようになります。

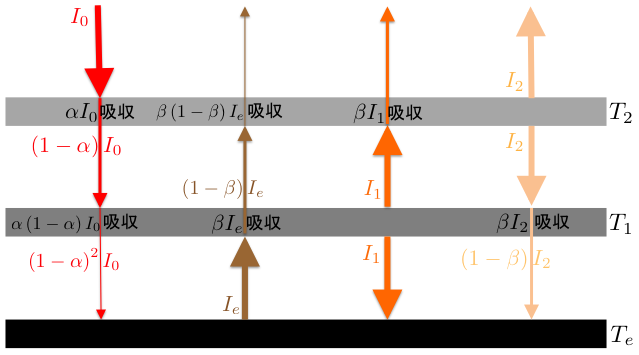
　まず地表のエネルギー収支を考えます。 先ほどまでと同様、2 つの大気層を通過した後に地表に到達する太陽放射は \(\left(1-\alpha\right)^{2}I_{0}\) です。 また、大気層 1 からの輻射は全て吸収します。 さらに、大気層 2 からの輻射は大気層 1 で \(\beta\) 分だけ吸収されるため、地表に届くのは \(\left(1-\beta\right)I_{2}\)となります。 そして輻射をしているため、地表のエネルギー収支は以下のようになります。 \begin{align*} \left(1-\alpha\right)^{2}I_{0}+I_{1}+\left(1-\beta\right)I_{2}=\Ie \end{align*}

　次に大気層 1 を考えます。 こちらも受け取る太陽放射は先ほどと同じです。 地表からの輻射は、\(\beta\) 分だけ受け取って残りは透過します。 同様に、大気層 1 からの輻射も \(\beta\) 分だけ受け取って残りは透過します。 そして上下に輻射をしているため、エネルギー収支は以下のように書けます。 \begin{align*} \alpha\left(1-\alpha\right)I_{0}+\beta\Ie+\beta I_{2}=2I_{1} \end{align*}

　大気層 2 は、太陽からの放射は \(\alpha\) 分だけ受け取ります。 大気層 1 からの輻射は \(\beta\) 分だけ受け取って残りは透過します。 地表からの輻射は、大気層 1 を通過した後の輻射を \(\beta\) 分吸収します。 そして上下に輻射をしているため、エネルギー収支は以下のように書けます。 \begin{align*} \alpha I_{0}+\beta I_{1}+\beta\left(1-\beta\right)\Ie=2I_{2} \end{align*}

2 層大気モデルでの表面温度と大気温度

　3 元連立方程式を行列を用いて解きます。 解くべき方程式を整理すると \begin{align*} I_{1}+\left(1-\beta\right)I_{2}-\Ie &= -\left(1-\alpha\right)^{2}I_{0}\\ -2I_{1}+\beta I_{2}+\beta \Ie &= -\alpha\left(1-\alpha\right)I_{0}\\ \beta I_{1}-2I_{2}+\beta\left(1-\beta\right)\Ie &= -\alpha I_{0} \end{align*} となるので、行列の形にすると \begin{align*} \left( \begin{array}{ccc} 1 & 1-\beta & -1 \\ -2 & \beta & \beta \\ \beta & -2 & \beta\left(1-\beta\right) \end{array} \right) \left( \begin{array}{c} I_{1} \\ I_{2} \\ \Ie \end{array} \right) = \left( \begin{array}{c} -\left(1-\alpha\right)^{2}I_{0} \\ -\alpha\left(1-\alpha\right)I_{0} \\ -\alpha I_{0} \end{array} \right) \end{align*} となります。

　2 行目 + 1 行目 × 2、3 行目 - 1 行目 × \(\beta\) という操作を行うと、 \begin{align*} \left( \begin{array}{ccc} 1 & 1-\beta & -1 \\ 0 & 2-\beta & -2+\beta \\ 0 & \beta^{2}-\beta-2 & -\beta^{2}+2\beta \end{array} \right) \left( \begin{array}{c} I_{1} \\ I_{2} \\ \Ie \end{array} \right) = \left( \begin{array}{c} -\left(1-\alpha\right)^{2}I_{0} \\ \left(-\alpha^{2}+3\alpha-2\right)I_{0} \\ \left[-\alpha+\beta\left(1-\alpha\right)^{2}\right] I_{0} \end{array} \right) \end{align*}

　2 行目を \(\left(2-\beta\right)\) で割ると、 \begin{align*} \left( \begin{array}{ccc} 1 & 1-\beta & -1 \\ 0 & 1 & -1 \\ 0 & \beta^{2}-\beta-2 & -\beta^{2}+2\beta \end{array} \right) \left( \begin{array}{c} I_{1} \\ I_{2} \\ \Ie \end{array} \right) = \left( \begin{array}{c} -\left(1-\alpha\right)^{2}I_{0} \\ \frac{-\alpha^{2}+3\alpha-2}{2-\beta}I_{0} \\ \left[-\alpha+\beta\left(1-\alpha\right)^{2}\right] I_{0} \end{array} \right) \end{align*}

　3 行目 - 2 行目 × \(\left(\beta^{2}-\beta-2\right)\) という操作をすると \begin{align*} \left( \begin{array}{ccc} 1 & 1-\beta & -1 \\ 0 & 1 & -1 \\ 0 & 0 & \beta-2 \end{array} \right) \left( \begin{array}{c} I_{1} \\ I_{2} \\ \Ie \end{array} \right) = \left( \begin{array}{c} -\left(1-\alpha\right)^{2}I_{0} \\ \frac{-\alpha^{2}+3\alpha-2}{2-\beta}I_{0} \\ \left(-\alpha^{2}+\alpha\beta+2\alpha-\beta-2\right)I_{0} \end{array} \right) \end{align*} となり、上三角行列の形に変形出来ました。

　行列の 3 行目から即座に \(\Ie\) が求められ、 \begin{align*} \Ie=\frac{\alpha^{2}-\alpha\beta-2\alpha+\beta+2}{2-\beta}I_{0} \end{align*} となります。 また行列の 2 行目からは \begin{align*} I_{2}-\Ie=-\frac{\alpha^{2}+3\alpha-2}{2-\beta}I_{0} \end{align*} が得られるので、\(\Ie\) を代入すれば \begin{align*} I_{2}=\frac{\alpha+\beta-\alpha\beta}{2-\beta}I_{0} \end{align*} が得られます。 行列の 1 行目からは \begin{align*} I_{1}+\left(1-\beta\right)I_{2}-\Ie=-\left(1-\alpha\right)^{2}I_{0} \end{align*} が得られるため、\(\Ie\)、\(I_{2}\) を代入して整理すれば \begin{align*} I_{1}=\frac{\alpha^{2}\beta-\alpha\beta^{2}-\alpha^{2}+\beta^{2}-\alpha\beta+\alpha+\beta}{2-\beta}I_{0} \end{align*} となり、解が得られました。

　行列を用いた連立方程式の解法は、大学の線形代数学で学ぶことが出来ます。 詳細は、線形代数学 (線型代数学) の教科書や、それらについて解説しているサイト等を参考にしてください。

参考文献