最もシンプルなモデル

　まずはスタートとして、最もシンプルな以下のケースを考えます。

　これらはかなり雑な仮定ではありますが、1 つ目の仮定については太陽放射のほとんどは可視光線と赤外線であり、可視光線は大気に対して透明なのでほとんどが地表まで到達すると考える事ができます。 近赤外線は大気による吸収はありますが、第ゼロ近似としては悪くありません。

　2 つ目の仮定について、地球からの熱輻射のピーク値は、地表の温度を 288 K (15℃) とすると、ウィーンの変位則(Wien's displacement law) より \begin{align*} \lambda_{\rm max}\simeq\frac{2900}{T\left(=288\,{\rm K}\right)}\,{\rm \mu m}\simeq 10\,{\rm \mu m} \end{align*} となり、遠赤外線領域であることが分かります。 (Wien の発音は「ヴィーン」が原語であるドイツ語読みに近いですが、慣習的に英語読みの「ウィーン」を用いる場合も多いです。) この波長域の電磁波も全て大気に吸収されるわけではありませんが、大部分は大気に吸収されるためこちらも近似としては悪くないと期待出来ます。 これらの仮定をもとに、大気層と地表でのエネルギー収支からそれぞれの温度を計算します。

　エネルギーのやりとりが釣り合い、平衡状態になった地表の温度を \(\Te\)、大気層の温度を \(T_{1}\) とします。 温度に応じた輻射フラックスは \(\Ie=\sigma\Te^{4}\)、\(I_{1}=\sigma T_{1}^{4}\) となります。 考えるのは以下の概略図のような状況です。

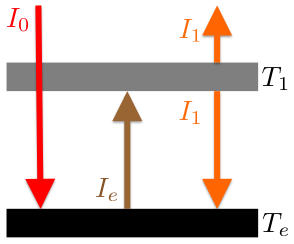
　地表は、太陽からの放射と大気層からの放射を受け取っています。 そして熱輻射をしてエネルギーを放出しているため、地表のエネルギー収支は以下のように書けます。 \begin{align*} I_{0}+I_{1}=\Ie \end{align*}

　大気層は、地表からの輻射を全て受け取り、上下に輻射をしているため、エネルギー収支は以下のようになります。 \begin{align*} \Ie=2I_{1} \end{align*}

　この 2 式を連立方程式として解くと、大気層からの輻射と地表からの輻射は、 \begin{align*} I_{1}&=I_{0}\\ \Ie&=2I_{0} \end{align*} と、太陽からの入射フラックスを用いて表すことができます。 \(I_{0}\)、\(I_{1}\)、\(\Ie\) にそれぞれ代入して整理すると、 \begin{align*} T_{1}^{4}&=T_{0}^{4}\\ \Te^{4}&=2T_{0}^{4} \end{align*} となります。 従って大気層と地表の温度は、大気が無い場合の平衡温度を用いて \begin{align*} T_{1}&=T_{0}\\ \Te&=2^{1/4}T_{0} \end{align*} と表す事ができます。

　この仮定の下での地表の温度は、大気が無い場合の平衡温度の \(2^{1/4}\) 倍になることが分かります。

　具体的な値を代入して温室効果による温度上昇効果を確かめてみます。 地球の平衡温度 255 Kを代入すると、大気層の温度は同じ 255 K、地表の温度は 303 Kとなり、大気の温室効果によって表面温度が 48 K上昇していることが分かります。 303 Kはおよそ 30℃ であるため、平衡温度よりは高くなるものの、実際の地球の平均的な気温である 15℃ は上回っています。 これは、「地表からの放射は全て大気に吸収される」という仮定によって、温室効果を過大評価している事が原因です。

　先ほどの最もシンプルなモデルでは、温室効果の再現は出来ましたが実際の地球の温度より高くなってしまいました。 現実には、地球からの遠赤外線を中心とした熱輻射は全て大気に吸収されるわけではなく、一部は大気を透過して宇宙空間へ逃げ出します。

　これを再現するために、地表からの熱輻射のうち一定の割合が宇宙空間へ"漏れ出す"というモデルを考えます。 太陽放射は同様に、全てが地表まで届くものとします。 考えるのは以下の状況です。

　この状態を表した概略図は以下のようになります。

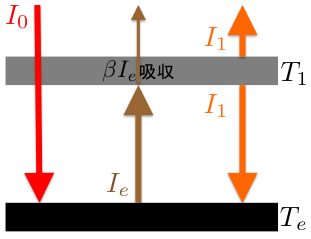
　地表のエネルギー収支は先ほどと同様で、以下のようになります。 \begin{align*} I_{0}+I_{1}=\Ie \end{align*}

　一方、大気層は地表からの輻射 \(\Ie\) のうち \(\beta\) 分だけを受け取り、上下に放射をしてエネルギーを失っているため、大気層のエネルギー収支は以下のようになります。 \begin{align*} \beta\Ie=2I_{1} \end{align*}

　同様にこの 2 式を連立方程式として解き、輻射を代入して温度で表すと \begin{align*} T_{1}^{4}&=\frac{\beta}{2-\beta}T_{0}^{4}\\ \Te^{4}&=\frac{2}{2-\beta}T_{0}^{4} \end{align*} となります。 よって、大気層と地表の温度は、大気の吸収率を \(\beta\) とすると以下のように表すことができます。 \begin{align*} T_{1}&=\left(\frac{\beta}{2-\beta}\right)^{1/4}T_{0}\\ \Te&=\left(\frac{2}{2-\beta}\right)^{1/4}T_{0} \end{align*}

　ここで \(\beta=1\) とした場合が最もシンプルなモデルの状況に対応していて、\(\beta=1\) を代入すると同じ結果になっている事が確認出来ます。

　\(\beta\) が 1 より小さい値を持つことによって、地表の温度の係数が \(2^{1/4}\) より小さくなります。 大気層からの"漏れ"がある分だけ、地表と大気層両方の平衡温度が下がっているという結果になっていることが分かります。

　一番最初のシンプルなモデルで起きた、地表の温度が現実よりもかなり高くなるという問題は、地球放射は大気に全て吸収されずに"漏れ"があるという事実をモデルに取り入れる事で回避出来ることがわかりました。 先ほどの \(\beta=0.8\) という値は、地表からの熱輻射のうち 80% は大気に吸収されているという状況を意味しています。 一番最初に仮定した、地球が放射する遠赤外線は大気に全て吸収されるという仮定は正しくはありませんが、近似としては近かったと言えます。 ではもう一つの仮定はどうでしょうか。

　ここまでのモデルでは、太陽からの放射は大気には吸収されずに地表に届くという状況を考えていました。 可視光線は実際にほとんど大気に対して透明ですが、近赤外線は必ずしもそうとは限りません。 例えば水分子は近赤外領域に強い吸収帯を持っているため、太陽からの近赤外線の一部は大気中の水蒸気によって強い吸収を受けます。

　そこで、先ほどのモデルに加えて、太陽からの放射も一部が大気に吸収されるという状況を考えます。 ここでの仮定は以下の通りです。

　この状況の概略図は以下のようになります。

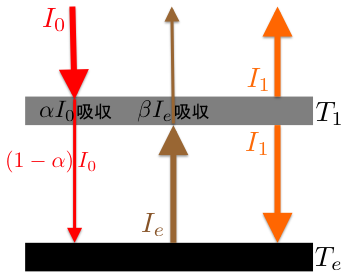
　この場合、地表が受け取ることが出来る太陽放射は、大気層で吸収された分を差し引いた \(\left(1-\alpha\right)I_{0}\) であり、また大気層からの輻射を受け取っています。 そして \(\Ie\) を放射しているため、地表のエネルギー収支は以下のようになります。 \begin{align*} \left(1-\alpha\right)I_{0}+I_{1}=\Ie \end{align*}

　大気層は、太陽からの輻射のうち \(\alpha\) をかけた分だけを受け取り、また地表からの輻射のうち \(\beta\) をかけた分だけを受け取っています。 そして上下に放射しているため、大気層のエネルギー収支の式は以下のように書けます。 \begin{align*} \alpha I_{0}+\beta\Ie=2I_{1} \end{align*}

　この 2 式を解くと \begin{align*} T_{1}^{4}&=\frac{\alpha+\beta-\alpha\beta}{2-\beta}T_{0}^{4}\\ \Te^{4}&=\frac{2-\alpha}{2-\beta}T_{0}^{4} \end{align*} となるため、それぞれの温度は次の式で表せます。 \begin{align*} T_{1}&=\left(\frac{\alpha+\beta-\alpha\beta}{2-\beta}\right)^{1/4}T_{0}\\ \Te&=\left(\frac{2-\alpha}{2-\beta}\right)^{1/4}T_{0} \end{align*}

　これが、1 層大気モデルによる、太陽放射の吸収と地表からの放射の吸収の両方を考慮した温室効果となります。

　太陽放射が大気層に全く吸収されない状態は \(\alpha=0\) の極限であり、これを代入すると一つ前の結果と一致することが分かります。 また、大気層による太陽放射の吸収が全く無く、地表からの放射は全て大気に吸収されるというのは \(\alpha=0\)、\(\beta=1\) の極限であり、これらを代入すると一番最初の結果とも一致します。

　ここで、\(\alpha=0.2\)、\(\beta=0.9\) を代入すると、大気層の温度は 244 K = -29℃ となります。 地表の温度は 288 K = 15℃ となり、実際の温度とほぼ一致することが分かります。

　このモデルは、太陽放射の大気による吸収と、地球の熱輻射の大気による吸収の両方が入っているため、よりもっともらしいモデルだろうと考えられます。 吸収率の値から、太陽放射の 20% が大気に吸収され、地球からの熱輻射のうち 90% が大気に吸収されると考えると最も良く合うということになります。 一番最初のモデルでは、太陽放射の吸収率は 0%、地球からの熱輻射の吸収率は 100% としていることになり、この部分の違いが結果として得られた表面温度のずれに繋がっていると考えることができます。

　実際には、大気による吸収率は波長によって大きく異なり、また大気中での散乱などの影響も考えなければならないため、精密な計算には輻射輸送を扱う必要があります。 しかしこの単純な1層大気モデルでも、大気の温室効果を十分に取り入れる事が出来て便利であるため、温室効果の説明の際にはしばしば使われるモデルです。

1 層大気モデルでの温室効果とその考察

　上で求めた 1 層大気モデルによる温室効果は、地球のような大気を持つ惑星に対してはかなり良い結果を与えます。 仮定は非常にシンプルですが、天体の大気次第では温室効果について良い見積もりを行うことができます。

　参考として火星の平衡温度を計算してみます。 火星の軌道長半径 1.524 AU、ボンドアルベド 0.16 を平衡温度を求める式に代入すると、火星の平衡温度は 216 K となります。 この温度は、既に火星の平均的な温度とほぼ同じであるため、火星では大気による温室効果は極めて弱いという推察が出来ます。

　火星の平均的な大気圧は 600 Pa であり、地球の大気圧 (101325 Pa = 1013.15 hPa = 1 気圧) のわずか 0.6% です。 このような極めて薄い大気では、温室効果は地球と比べると非常に弱くなります。

　次に温室効果が最大になる状況を考えてみます。 1層大気モデルでの温室効果を考慮した表面温度は \begin{align*} \Te=\left(\frac{2-\alpha}{2-\beta}\right)^{1/4}T_{0} \end{align*} と書けるのでした。 この温度が最大になるのは、太陽放射が直接地表へ到達し、地球からの熱輻射は全て大気に吸収されるという場合、すなわち \(\alpha=0\) かつ \(\beta=1\) の時です。 この時の表面温度は \begin{align*} \Te=2^{1/4}T_{0} \end{align*} となります。
　この式から分かる事は、1 層大気モデルを考えた時は、最大の温室効果を仮定しても平衡温度の \(2^{1/4}\) 倍にしかならないということです。