対流不安定の条件のページでは、流体内のブロブを微小距離上昇させた状況の密度変化を考え、対流不安定か対流安定かの条件を導出しました。 組成の勾配を考えない場合は Schwarzschild criterion (シュヴァルツシルトの判定条件) が得られ、 組成の勾配まで考えた場合は Ledoux criterion (ルドゥーの判定条件) が得られました。
一方で、この 2 つの判定条件は、流体に関する基礎方程式からも導くことができます。 具体的には、ある条件の下での基礎方程式について線形解析を行います。 方程式の変数に微小な摂動項を含む式を代入し、その摂動の振幅が時間とともに増大する解があればその系は不安定、 摂動を与えてもその振幅が振動するのみ、あるいは時間とともに減衰してしまう場合はその系は安定と判別されます。
また、Schwarzschild criterion と Ledoux criterion の両者では、熱の拡散と組成の拡散の効果は無視していましたが、現実には熱も組成も拡散します。
基礎方程式の線形解析からは、組成の拡散まで含めたより一般的な判定条件を導出する事も出来ます。
ここでは、その線形解析について簡単に紹介したいと思います。
目次:
関連ページ:
流体の基礎方程式
鉛直上向きに \(z\) 軸を取り、\(z\)軸方向に温度勾配や組成勾配がある状況を考えます。 \(x\)、\(y\) 方向には流体は一様であるとします。 また、粘性拡散、熱拡散、組成拡散のそれぞれの効果を考慮します。
流体の運動方程式は、 \begin{align*} \frac{\del\bm{u}}{\del t} + \left(\bm{u}\cdot\nabla\right)\bm{u}=-\frac{1}{\rho_{0}}\nabla P + \frac{\rho}{\rho_{0}}\bm{F} + \nu\nabla^{2}\bm{u} \end{align*} です。 ここで \(\bm{u}\) は流体の速度ベクトルであり、各成分を \(\bm{u}=\left(u,\,v,\,w\right)\) と書く事とします。 また、\(\rho\) は流体の密度、\(\rho_{0}\) はバックグラウンドの平均的な密度、\(P\) は流体の圧力です。 また、\(\bm{F}\) は流体に働く外力、\(\nu\) は流体の粘性係数を表します。
熱に関する方程式は、 \begin{align*} \frac{\del T}{\del t} + \left(\bm{u}\cdot\nabla\right)T + \left(\toz-\tozad\right)w = \kappat\nabla^{2}T \end{align*} となります。 \(T\)は流体の温度、\(\toz\) は温度の \(z\) 微分、つまり温度の勾配を表します。 また、添字 ad は断熱変化を表す添字であり、\(\tozad\) は断熱温度変化を表す文字です。 \(\kappat\) は熱拡散係数を表し、温度の拡散の度合いを表す係数です。
組成に関する方程式は、 \begin{align*} \frac{\del\mu}{\del t} + \left(\bm{u}\cdot\nabla\right)\mu + \muoz w = \kappamu\nabla^{2}\mu \end{align*} となります。 \(\mu\) は流体の平均分子量、\(\muoz\) は温度の時と同じく、平均分子量の \(z\) 方向の勾配を表します。 \(\kappamu\) は組成拡散係数を表します。
運動方程式、熱に関する方程式、組成に関する方程式は以上ですが、簡単のため流体は非圧縮性であると仮定します。 非圧縮性流体は以下の関係を満たします。 \begin{align*} \nabla\cdot\bm{u}=0 \end{align*} 流体が非圧縮であるということは、流体の密度変化が起きないという事になります。 このような場合は上昇しても流体素片は膨張せず、浮力が働かないことになります。 そのため本来はこの状態では対流が発生出来ないことになります。 そこで、非圧縮流体を考えながらも、運動方程式には密度変化による浮力が働くような近似を行います。 これは、流体の密度変化は起きないが、運動方程式の浮力項のみには密度変化による効果を考慮する、という近似です。 このような近似は Boussinesq approximation (ブシネスク近似) と呼ばれ、対流の議論をする時にしばしば用いられる近似です。
Boussinesq approximation では、流体密度の変化は \begin{align*} \rho=\rho_{0}\left(-\alpha T + \beta\mu\right) \end{align*} と書き表すことが出来ます。 これらの係数は、流体が理想気体の場合は \(\alpha=1/T_{0}\)、\(\beta=1/\mu_{0}\) となります。
また、流体に働く外力には、\(z\) の負の方向に働く重力のみを考え、 \begin{align*} \bm{F}=-g\bm{e_{z}} \end{align*} とします。 \(g\) はその場所での重力加速度です。 Boussinesq approximation による密度変化の項と、外力の項を運動方程式に代入すると、 \begin{align*} \frac{\del\bm{u}}{\del t} + \left(\bm{u}\cdot\nabla\right)\bm{u} = -\frac{1}{\rho_{0}}\nabla P + \left(-\alpha T + \beta\mu\right)g\bm{e_{z}} + \nu\nabla^{2}\bm{u} \end{align*} が得られます。
以上より、線形解析に用いる基礎方程式は、
これらの方程式を全て成分ごとに書き下すと、以下のようになります。
これらの式をもとに線形解析を行い、流体の不安定性について調べて行きます。
次に基礎方程式に摂動を与えます。
微小な摂動を、変数を \(V\) として
\begin{align*}
V=\hat{V}e^{ilx+imy+ikz+\lambda t}
\end{align*}
の形で与えます。
\(V\) に入るのは、\(u,\,v,\,w,\,T,\,\mu,\,P\) の各 6 変数です。
この式を基礎方程式に代入して整理することによって、分散関係を求めます。
まず \eqref{incomp} 式に、\(u,\,v,\,w\) を代入して式を整理すると、
\begin{align}
l\hat{u}+m\hat{v}+k\hat{w}=0
\tag{6'}
\label{incomp2}
\end{align}
が得られます。
続いて、\eqref{eomx} 式に \(u,\,v,\,w,\,P\) を代入します。
\eqref{incomp2} 式を用いて整理すると、
\begin{align}
\lambda\hat{u}=-\frac{1}{\rho_{0}}il\hat{P}-\nu K^{2}\hat{u}
\tag{1'}
\label{eomx2}
\end{align}
が得られます。
ただし、\(K^{2}=l^{2}+m^{2}+k^{2}\) です。
\eqref{incomp2} 式を代入した結果から分かるように、\(\left(\bm{u}\cdot\nabla\right)V\) の形をした項 (左辺の第 2 項) はゼロになります。
\eqref{eomy} 式に \(u,\,v,\,w,\,P\) を代入して整理すると、
\begin{align}
\lambda\hat{v}=-\frac{1}{\rho_{0}}im\hat{P}-\nu K^{2}\hat{v}
\tag{2'}
\label{eomy2}
\end{align}
が得られます。
また、\eqref{eomz} 式に \(u,\,v,\,w,\,P,\,T,\,\mu\) を代入すると、
\begin{align}
\lambda\hat{w}=-\frac{1}{\rho_{0}}ik\hat{P}+\left(\alpha\hat{T}-\beta\hat{\mu}\right)g-\nu K^{2}\hat{w}
\tag{3'}
\label{eomz2}
\end{align}
となります。
同様に、\eqref{eot} 式に \(T,\,u,\,v,\,w\) を代入して整理すると
\begin{align}
\lambda\hat{T}+\left(\toz-\tozad\right)\hat{w}=-\kappat K^{2}\hat{T}
\tag{4'}
\label{eot2}
\end{align}
となり、\eqref{eomu}式に \(\mu,\,u,\,v,\,w\) を代入して整理すると
\begin{align}
\lambda\hat{\mu}+\muoz\hat{w}=-\kappamu K^{2}\hat{\mu}
\tag{5'}
\label{eomu2}
\end{align}
が得られます。
これらの \eqref{eomx2}〜\eqref{incomp2} 式から \(\hat{V}\) (ハットが付いている文字全て) を消去することによって、分散関係が得られます。
式 \eqref{eomx2} と \eqref{eomy2} を \(\hat{u}\) と \(\hat{v}\) の式に直し、\eqref{incomp2} に代入すると、
\begin{align}
\hat{P}=\frac{\rho_{0}\left(\lambda+\nu K^{2}\right)}{i\left(l^{2}+m^{2}\right)}k\hat{w}
\tag{6''}
\label{incomp3}
\end{align}
が得られます。
式 \eqref{eot2}、\eqref{eomu2} を \(\hat{T}\)、\(\hat{\mu}\) の式に直して式 \eqref{eomz2} に代入し、更に式 \eqref{incomp3} を代入すると \(\hat{w}\) が消去でき、
\begin{align*}
\left(\lambda+\nu K^{2}\right)=-\frac{k^{2}}{l^{2}+m^{2}}\left(\lambda+\nu K^{2}\right)
-\alpha g\frac{\toz-\tozad}{\lambda+\kappat K^{2}}+\beta g\frac{\muoz}{\lambda+\kappamu K^{2}}
\end{align*}
が得られます。
これを整理すると
まずは、組成勾配が存在せず、熱拡散も組成拡散も無い最もシンプルな状況を考えます。
この状況での不安定条件は、Schwarzschild criterion と一致するはずです。
組成勾配が存在しないという条件は \(\muoz=0\) で与えられます。
また、熱拡散と組成拡散が無いという条件は、\(\kappat=\kappamu=0\) となります。
これらを分散関係の式 \eqref{disp} に代入すると、
\begin{align*}
\lambda^{2}+\nu K^{2}\lambda+g\alpha\frac{l^{2}+m^{2}}{K^{2}}\left(\toz-\tozad\right)=0
\end{align*}
となります。
この 2 次方程式は容易に解くことができて、解は
\begin{align*}
\lambda=\frac{-\nu K^{2}\pm\sqrt{\nu^{2}K^{4}-4g\alpha\frac{l^{2}+m^{2}}{K^{2}}\left(\toz-\tozad\right)}}{2}
\end{align*}
となります。
系の安定性、不安定性は、この解の実数部分がどうなっているかによって変わります。
与えた摂動の元の形は
\begin{align*}
V=\hat{V}e^{ilx+imy+ikz+\lambda t}
\end{align*}
です。
\(\lambda\) の虚数部分は、元の形に代入すると指数関数の肩に虚数が乗っている状態になるため、三角関数の形で書くことができます。
すなわち振動する部分です。
一方、実部が正の場合は振幅が指数関数的に増大する解になるため、不安定な解が存在することになります。
実部が負であれば振幅が指数関数的に減衰するため、安定と判断出来ます。
この場合、根号の内部が負の場合は、λの実数部分は \(-\nu K^{2}\) のみで負であるため、与えた摂動は指数関数的に減衰して安定であることが分かります。
一方、根号の内部が正であり、かつ
\begin{align*}
\nu K^{2} \lt \sqrt{\nu^{2}K^{4}-4g\alpha\frac{l^{2}+m^{2}}{K^{2}}\left(\toz-\tozad\right)}
\end{align*}
となっていれば、\(\lambda\) の実部が正になるため摂動は指数関数的に増大し、不安定になります。
両辺を 2 乗してこの不等式を解くと、
\begin{align*}
\toz-\tozad \lt 0
\end{align*}
となります。
これは Schwarzschild criterion である
\begin{align*}
\nabla_{T}-\nabla_{\rm ad} \gt 0
\end{align*}
と同等の式 (不等号の向きに注意) であり、基礎方程式の線形解析から Schwarzschild criterion が導出出来ました。
次に、組成勾配がある場合を考えます。
ここでも先程と同様に、熱拡散と組成拡散は無視します。
すなわち、\(\kappat=\kappamu=0\) とします。
この条件での不安定条件は、Ledoux criterion と一致するはずです。
式 \eqref{disp} に代入すると、分散関係は
\begin{align*}
\lambda^{2}+\nu K^{2}\lambda+g\frac{l^{2}+m^{2}}{K^{2}}\left(\alpha\left(\toz-\tozad\right)-\beta\muoz\right)=0
\end{align*}
となります。
先程と全く同様に同様に 2 次方程式を解き、不安定のための条件を求めると、
\begin{align*}
\alpha\left(\toz-\tozad\right)-\beta\muoz \lt 0
\end{align*}
が得られます。
ここで、例として理想気体の場合を考えます。
Boussinesq approximation の関係より、理想気体では \(\alpha=1/T_{0}\)、\(\beta=1/\mu_{0}\) という関係式があります。
これらを代入すると、不安定のための条件は
\begin{align*}
\frac{\toz}{T_{0}}-\frac{\tozad}{T_{0}}-\frac{\muoz}{\mu_{0}} \lt 0
\end{align*}
となります。
ここで、添字の \(0z\) は \(z\) 微分であることを思い出すと、
\begin{align*}
\frac{\toz}{T_{0}}=\frac{1}{T_{0}}\frac{dT}{dz}=\frac{d\ln T}{dz}
\end{align*}
と書くことができるため、不安定のための条件は
\begin{align*}
\frac{d\ln T}{dz}-\left(\frac{d\ln T}{dz}\right)_{\rm ad}-\frac{d\ln\mu}{dz} \lt 0
\end{align*}
と書き直すことができます。
これの両辺に \(dz/d\ln P\) をかけると、
\begin{align*}
\left(\frac{d\ln T}{d\ln P}\right)-\left(\frac{d\ln T}{d\ln P}\right)_{\rm ad}-\left(\frac{d\ln\mu}{d\ln P}\right) \gt 0
\end{align*}
となります。
\(dz/d\ln P\) は負であるため、不等号の向きに注意します。
この式は、理想気体の Ledoux criterion である
\begin{align*}
\nabla_{T}-\nabla_{\rm ad} \gt \nabla_{\mu}
\end{align*}
と一致します。
不安定性条件の式
\begin{align*}
\alpha\left(\toz-\tozad\right)-\beta\muoz \lt 0
\end{align*}
において、
組成勾配の正負まで考慮した、より一般的な考察は後ほど行います。
最後に、本題である熱拡散、組成拡散が入った場合の系の不安定性について見て行きます。
まず、少々天下り的ではありますが、線形解析の安定性条件である Hurwitz stability criterion (フルビッツの安定判別法) を用います。
これは、分散関係が
\begin{align*}
c_{0}k^{3}+c_{1}k^{2}+c_{2}k+c_{3}=0
\end{align*}
で与えられるとき、
各係数が
\begin{align*}
c_{0},\,c_{1},\,c_{2},\,c_{3}\geq0
\end{align*}
かつ
\begin{align*}
\left|
\begin{array}{ll}
c_{1} & c_{0} \\
c_{3} & c_{2}
\end{array}
\right|
\geq0
\end{align*}
を満たすときは安定である、というものです。
実際の Hurwitz stability criterion は n 次の分散関係一般について成り立つものであり、ここに示したものは 3 次式の場合になります。
先程導出した分散関係 \eqref{disp} は
\begin{align*}
\frac{K^{2}}{l^{2}+m^{2}}\left(\lambda+\nu K^{2}\right)\left(\lambda+\kappat K^{2}\right)\left(\lambda+\kappamu K^{2}\right)+\alpha g\left(\toz-\tozad\right)\left(\lambda+\kappamu K^{2}\right)-\beta g \muoz\left(\lambda+\kappat K^{2}\right)=0
\end{align*}
でした。
これを展開して各係数を求めると、計算が面倒ですが
\begin{align*}
c_{0}&=\frac{K^{2}}{l^{2}+m^{2}}\\
c_{1}&=\frac{K^{4}}{l^{2}+m^{2}}\left(\kappat+\kappamu+\nu\right)\\
c_{2}&=\frac{K^{6}}{l^{2}+m^{2}}\left(\kappat\kappamu+\kappamu\nu+\nu\kappat\right)+g\left(\alpha\left(\toz-\tozad\right)-\beta\muoz\right)\\
c_{3}&=\frac{K^{8}}{l^{2}+m^{2}}\kappat\kappamu\nu+g\alpha K^{2}\kappamu\left(\toz-\tozad\right)-g\beta K^{2}\kappat\muoz
\end{align*}
となります。
ここで、\(c_{0}\) と \(c_{1}\) は明らかに 0 以上です。
\(c_{2}\) は第 1 項は 0 より大きいですが、第 2 項は必ずしも正であるという保証はありません。
しかし、第 2 項をよく見ると、これは Ledoux criterion の形そのままであることが分かります。
第 2 項が負の時は Ledoux criterion で不安定ということであり、\(c_{2}\) も負になる場合があるため不安定なモードが存在することになります。
しかし、Ledoux criterion で不安定という事は、そもそも拡散の効果を考慮するまでもなく不安定であるということです。
今は、Ledoux criterion では安定と判断されるにも関わらず、拡散の効果によって不安定化され得る領域について考えたいため、ここでは第 2 項が正の場合のみを考えても良いことになります。
よって、\(c_{2}\) が正の場合のみを考えても問題ありません。
\(c_{3}\) についても、第 1 項は 0 より大きいですが、第 2 項以降は負になり得る項です。
Ledoux criterion に似た形状をしていますが、拡散係数があるため同じ形ではありません。
そのため \(c_{3}\) が正になる条件については考慮が必要です。
\(c_{3}\) が必ず正になるための条件は、
\begin{align}
\alpha\kappamu\left(\toz-\tozad\right)-\beta\kappat\muoz \gt 0
\tag{B}
\label{disp2}
\end{align}
です。
次に、行列式を計算して安定のための条件を求めると、こちらも計算は煩雑になりますが、うまく項を整理してやると
\begin{align*}
\frac{K^{10}}{l^{2}+m^{2}}\left(\kappat+\kappamu\right)\left(\kappamu+\nu\right)\left(\nu+\kappat\right)
+\frac{K^{4}}{l^{2}+m^{2}}\left(\kappamu+\nu\right)\beta\muoz\left(\frac{\kappat+\nu}{\kappamu+\nu}\frac{\alpha}{\beta}\frac{\toz-\tozad}{\muoz}-1\right)\geq 0
\end{align*}
の時は系が安定であることが分かります。
ここで、\(K^{10}\) の項は明らかに正になるため、\(K^{4}\) の項について考えます。
系が確実に安定であるためには、
\begin{align*}
\frac{K^{4}}{l^{2}+m^{2}}\left(\kappamu+\nu\right)\beta\muoz\left(\frac{\kappat+\nu}{\kappamu+\nu}\frac{\alpha}{\beta}\frac{\toz-\tozad}{\muoz}-1\right)\geq 0
\end{align*}
を満たしている必要があります。
ここで、先程導入した式 \eqref{densityratio} density ratio を用いてこの安定条件を評価します。
また、流体力学の無次元量である、Prandtl number (プラントル数) \({\rm Pr}\equiv\nu/\kappat\) と、Lewis number (ルイス数) の逆数である \(\tau\equiv\kappamu/\kappat\) を導入します。
プラントル数は粘性拡散と熱拡散の比、ルイス数 (の逆数) は組成拡散と熱拡散の比となっています。
これらを代入して整理すると、安定のための条件は、
\begin{align}
\muoz\left(\frac{{\rm Pr}+1}{{\rm Pr}+\tau}R_{0}-1\right)\gt0
\tag{C}
\label{disp3}
\end{align}
と書くことができます。
式 \eqref{disp2} と \eqref{disp3} の両方を満たす場合は系は安定です。
まず、組成勾配が負である場合を考えます。
つまり \(\muoz \lt 0\) の場合です。
これは、下層は平均分子量が大きくて重く、上層が平均分子量が小さく軽いため、組成勾配が系の安定化にはたらく状況に相当します。
この場合、まず \eqref{disp2} 式の条件は
\begin{align*}
\frac{\kappamu}{\kappat}\frac{\alpha}{\beta}\frac{\toz-\tozad}{\muoz}-1 \lt 0
\end{align*}
となります。
これを、density ratio とルイス数の逆数を用いて表すと、
\begin{align}
R_{0}^{-1} \gt \tau
\tag{B2}
\label{b2}
\end{align}
が得られます。
次に、式 \eqref{disp3} の条件を考えます。
式 \eqref{disp3} からは、
\begin{align}
R_{0}^{-1}\geq\frac{{\rm Pr}+1}{{\rm Pr}+\tau}
\tag{C2}
\label{c2}
\end{align}
が得られます。
式 \eqref{b2} と式 \eqref{c2} を両方満たす状況が、全てのモードが安定であるための条件です。
そのため、どちらの条件が厳しいか調べる必要があります。
両条件の大小を比較すると、
\begin{align*}
\frac{{\rm Pr}+1}{{\rm Pr}+\tau}-\tau&=\frac{\kappat+\nu}{\kappamu+\nu}-\frac{\kappamu}{\kappat}\\
&=\frac{\left(\kappat-\kappamu\right)\left(\kappat-\kappamu+\nu\right)}{\kappat\left(\kappamu+\nu\right)}
\end{align*}
となります。
天体の内部では \(\tau\sim10^{-7}\) 程度と考えられていますが、ルイス数の定義よりこれはすなわち \(\kappamu/\kappat\sim10^{-7}\) であるということです。
そのため \(\kappat\gg\kappamu\) であることが分かります。
また一般に、熱拡散は組成拡散よりも大きいと見なせるため、常に \(\kappat \gt \kappamu\) とすることが出来ます。
そのため、条件の比較は
\begin{align*}
\frac{{\rm Pr}+1}{{\rm Pr}+\tau} \gt \tau
\end{align*}
となり、式 \eqref{c2} の方が厳しい条件になります。
よって、全てのモードで安定であるための条件は
\begin{align*}
R_{0}^{-1}\geq\frac{{\rm Pr}+1}{{\rm Pr}+\tau}
\end{align*}
であることが分かります。
従って、不安定なモードが存在するための条件は、安定であるための条件の逆の
\begin{align*}
R_{0}^{-1} \lt \frac{{\rm Pr}+1}{{\rm Pr}+\tau}
\end{align*}
となります。
次に、組成勾配が正である場合を考えます。
すなわち \(\muoz \gt 0\) の場合です。
上層が平均分子量が大きくて重く、下層が平均分子量が小さくて軽い状況に対応していて、組成勾配が系を不安定化させる方向にはたらく系になっています。
この場合、まず式 \eqref{disp2} は
\begin{align*}
\frac{\kappamu}{\kappat}\frac{\alpha}{\beta}\frac{\toz-\tozad}{\muoz}-1 \gt 0
\end{align*}
となります。
ここで同様に density ratio とルイス数の逆数を使うと、
\begin{align*}
R_{0} \gt \frac{1}{\tau}
\tag{B3}
\label{b3}
\end{align*}
が得られます。
一方、式 \eqref{disp3} は
\begin{align*}
R_{0} \gt \frac{{\rm Pr}+\tau}{{\rm Pr}+1}
\tag{C3}
\label{c3}
\end{align*}
となります。
式 \eqref{b3} と \eqref{c3} を両方満たす条件が、全てのモードで安定であるための条件です。
同様にどちらの条件が厳しいか比較すると、
\begin{align*}
\frac{1}{\tau}-\frac{{\rm Pr}+\tau}{{\rm Pr}+1}=\frac{\left(\kappat-\kappamu\right)\left(\kappat+\kappamu+\nu\right)}{\kappat\left(\kappamu+\nu\right)} \gt 0
\end{align*}
となります。
従って
\begin{align*}
\frac{1}{\tau} \gt \frac{{\rm Pr}+\tau}{{\rm Pr}+1}
\end{align*}
となり、式 \eqref{b3} の方が厳しい条件となります。
よって、全てのモードで安定であるための条件は
\begin{align*}
R_{0} \gt \frac{1}{\tau}
\end{align*}
となります。
従って、不安定なモードが存在するための条件は、逆の
\begin{align*}
R_{0} \lt \frac{1}{\tau}
\end{align*}
となります。
組成勾配を考慮し、拡散を無視した場合の対流不安定性は Ledoux criterion で記述することができました。
また、熱拡散、組成拡散の両方を考慮した場合についても、線形解析から不安定条件を導出することができました。
パラメータとして density ratio (の逆数) を導入して系の不安定性を考慮すると、組成勾配が負の場合は、Ledoux criterion では
\(R_{0}^{-1} \lt 1\) の時は不安定であり、\(R_{0}^{-1} \gt 1\) の時は安定と判別されました。
しかし \(\tau\) が 1 より小さい場合は \(\left({\rm Pr}+1\right)/\left({\rm Pr}+\tau\right)\) は 1 より大きい値を取るため、拡散を無視した Ledoux criterion では安定と判別されても、拡散を考慮した条件では不安定と判別される \(R_{0}^{-1}\) の範囲が存在することになります。
一般に \(\tau \ll 1\) であり、例として恒星内部やガス惑星の内部では \(\tau\sim10^{-7}\) 程度の値を取る事が分かっています。
また、恒星内部やガス惑星内部では同様に \({\rm Pr} \ll 1\) です。
以上の結果をまとめて、density ratio の逆数をパラメータとして系を判別すると次のようになります。
Ledoux criterion で不安定な領域では対流が発達するため、大域的な対流によって熱が効率的に輸送されます。
また、拡散を考慮した上でなお安定な領域では対流は発達しないため静的な系になり、対流による熱輸送は発生しないことになります。
その中間の、Ledoux criterion では安定だが拡散の効果によって不安定化されるモードがある系では、
二重拡散対流 (double diffusive convection) と呼ばれる不安定が発達します。
2 種類の違う拡散、この場合は熱拡散と組成拡散が存在する事によって発生する現象なのでこのような名前が付けられています。
二重拡散対流が発達する系では、大域的な対流とは異なる過程での熱輸送と組成輸送が発生します。
組成勾配が負の場合、
\begin{align*}
1 \lt R_{0}^{-1} \lt \frac{{\rm Pr}+1}{{\rm Pr}+\tau}
\end{align*}
を満たす時に二重拡散対流が発達し得ます。
この場合、拡散による不安定化の影響で、細かく薄い層に分割された対流層が、何層も重なった構造を形成します。
この構造は層対流 (layered convection) と呼ばれます。
層対流では、各層の内部では対流によって熱が輸送されますが、層と層の境界部分では拡散によって熱が輸送されます。
そのため、対流によってかき混ぜられている各層の内部では、温度やエントロピー、組成は一様になりますが、
層と層の境界では温度や組成に飛びが見られ、階段状の構造になります。
また、全体的な熱輸送の効率は層の境界部分の拡散で決まるため、大域的な対流よりも熱輸送の効率は大きく落ちることになります。
また、一般に熱拡散係数は組成拡散係数よりも大きい(つまり熱拡散の方が組成拡散よりも速い)ため、層と層の境界である拡散界面 (diffusive interface) では熱の輸送の方が素早く行われます。
そのため、層対流は比較的安定であると考えられます。
層対流は、二重拡散対流での現象であるという意味を込めて二重拡散層対流 (double diffusive layered convection) と呼ばれることもあります。
組成勾配が正の場合、
\begin{align*}
1 \lt R_{0} \lt \frac{1}{\tau}
\end{align*}
を満たす時に二重拡散対流が発達し得ます。
温度勾配が負である場合を考え、この状況で起きる事を定性的に示します。
この場合、下層は高温で軽く、上層は低温で重いため、温度勾配は系を不安定化する方向にはたらきます。
また、下層は平均分子量は小さいため軽く、上層は平均分子量が大きく重いため、組成勾配によっても不安定化されます。
Ledoux criterion による安定のための条件は、温度勾配と組成勾配の合計と、断熱温度勾配と拮抗している事でした。
しかし、拡散の効果も考えるとそれだけでは安定のためには不十分です。
この場合、上層の重い部分の一部が下層へ向かって沈み込もうとし、また下層の軽い部分の一部は上層へ向かって昇ろうとします。
これらはそのまま指を伸ばすように沈み続ける、あるいは昇り続けるといった混合を起こすため、
フィンガー型対流 (fingering convection) と呼ばれます。
これら二重拡散対流による層対流やフィンガー型対流は、海洋で実際に存在する事が分かっています。
また、恒星やガス惑星内部でも発生している可能性があると考えられています。
海水の場合は、温度勾配と、塩分濃度の組成勾配があり、熱拡散と塩分濃度の拡散の 2 種類が存在するため、二重拡散対流が発生することがあります。
例として、まずは海水の温度勾配も塩分濃度勾配も正である場合を考えます。
この場合は下層は冷たくて重く、上層は熱くて軽いため、温度勾配は安定化にはたらきます。
しかし下層は低濃度で軽く、上層は高濃度で重いため組成勾配は系を不安定化しようとします。
Ledoux criterion で安定であれば大域的な対流は発達しませんが、拡散による効果で不安定化される状況であれば
上下方向に指を伸ばすようなフィンガー型対流による混合が発達します。
海水中でのこの混合を指してソルトフィンガー型対流と呼びます。
次に、温度勾配も塩分濃度勾配も負である場合を考えます。
この場合は真逆で、温度勾配は不安定化しようとしますが、組成勾配は安定化しようとします。
同じく Ledoux criterion で安定であれば大域的な対流は発達しませんが、拡散による効果で不安定化される状況であれば
薄い対流層がいくつも重なった層対流が発達します。
これらの海水中でのソルトフィンガー型対流と層対流は、実際に発生している事が測定から分かっています。
海水中での温度勾配と組成勾配による二重拡散対流の事を指して、熱塩対流 (thermohaline convection) と呼びます。
今は熱拡散と組成拡散の2種類を考えましたが、熱拡散が無く、2 種類の組成拡散がある場合でも同じ現象が発生します。
例えば拡散速度が異なる溶液が接している状況では、2 種類の組成拡散によってフィンガー型対流が発達します。
また、温度勾配と組成勾配が負で、Schwarzschild criterion では不安定だが Ledoux criterion では安定になる条件では、半対流や準対流 (semi-convection) と呼ばれる、一部分の混合が発生する事があり、どの程度の混合が起きるのかはその系の進化を考える上で重要になる事があります。
分散関係の導出
Schwarzschild criterion の導出
Ledoux criterion の導出
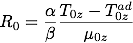
拡散が入った場合の不安定条件
負の組成勾配がある場合
正の組成勾配がある場合
不安定条件のまとめ
\(\displaystyle{0 \lt R_{0}^{-1} \lt 1}\)
・・・Ledoux criterion で対流不安定
\(\displaystyle{1 \lt R_{0}^{-1} \lt \frac{{\rm Pr}+1}{{\rm Pr}+\tau}}\)
・・・Ledoux criterion では安定だが拡散の効果により不安定
\(\displaystyle{R_{0}^{-1} \gt \frac{{\rm Pr}+1}{{\rm Pr}+\tau}}\)
・・・拡散を考慮した上でなお安定
正の組成勾配がある場合は、
\(\displaystyle{0 \lt R_{0} \lt 1}\)
・・・Ledoux criterion で対流不安定
\(\displaystyle{1 \lt R_{0} \lt \frac{1}{\tau}}\)
・・・Ledoux criterion では安定だが拡散の効果により不安定
\(\displaystyle{R_{0} \gt \frac{1}{\tau}}\)
・・・拡散を考慮した上でなお安定
負の組成勾配がある場合
正の組成勾配がある場合
二重拡散対流の実例
参考リンク:富山大学工学部材料機能工学科 材料プロセス工学研究室の HPより
(分かりやすいフィンガー型対流の動画があるのでリンクさせて頂きました)
2017年06月05日 更新