夜空の星の明るさを示す指標には、等級と言うものがあります。
夜空の中でも特に明るい星は1等星と呼ばれますが、この数字が小さいほど明るい星、大きいほど暗い星である事を表します。
また、等級にも定義によって様々な種類があり、地球から見た明るさを示すものとしては見かけの等級、距離によらず天体の明るさを比較する為の指標としての絶対等級などがあります。
ここでは、天体の見かけの等級と絶対等級について簡単に紹介します。
見かけの等級 (apparent magnitude)とは、文字の通り地球から見た時の天体の見かけの明るさを示す指標です。
本来は同じ明るさの天体であっても、近距離にあるものの見かけの明るさは明るく、遠方にあるものは暗く見えます。
また近距離であっても非常に暗い天体や、遠距離でも非常に明るい場合は、遠距離にある天体の方が明るく見える事があります。
このような、見かけの明るさの指標となるのが見かけの等級です。
現在では天体の明るさは定量的な評価が可能になっていますが、昔は目で見た時の明るさの違いという大まかな違いでの評価しか出来ませんでした。
そこで、夜空に見える恒星のうち最も明るいものを1等星、肉眼で観測出来る最も暗いものを6等星とし、1〜6の6段階で分類されるようになりました。
この分類方法を考案したのは古代ギリシアの天文学者であったヒッパルコスで、まだ紀元前のことです。
その後16世紀になって望遠鏡が開発されると、肉眼では見えない恒星も発見出来るようになり、より暗い恒星には7等星、8等星といった等級が与えられるようになりましたが、この段階では統一された基準は設けられていませんでした。
また、等級の値も整数のみで与えられるものでした。
現在まで使われている等級の定義を決定したのは、イギリスの天文学者のノーマン・ロバート・ポグソン (Norman Robert Pogson)です。
ポグソンが等級の定義を決めるより前に、同じくイギリスの天文学者であるジョン・ハーシェルによって、1等星の明るさが6等星の明るさのおよそ 100倍であることが示されていました。
(なおジョン・ハーシェルは、天王星とその衛星の発見や望遠鏡製作等で多数の業績を持つ天文学者、ウィリアム・ハーシェルの息子です。)
ポグソンはジョン・ハーシェルの研究結果を元にし、1等星の明るさは6等星の 100倍であり、1等級ごとの明るさの違いは 1001/5倍であると定義しました。
これは 1856年のことです。
1001/5 = 2.511886432... となるため、1等級ごとの違いはおよそ 2.512倍に相当するということになります。
このポグソンによる等級の定義によって、等級は定量的に評価出来るようになり、1〜6以外の等級、例えば6より大きな等級や0, 負の値の等級、整数値の間の小数値を持つ等級も表すことができるようになりました。
また、見かけの等級の比較の際にしばしば出てくる数値である 1001/5の事は、ポグソンに因んでポグソン比 (Pogson's ratio)と呼ばれます。
ポグソンが等級の定義を定めた事で、天体の見かけの明るさから等級を計算出来るようになりました。
ここでは、等級はどのように決まるか見て行きます。
ポグソンの定義では、等級が1異なるごとに明るさは 1001/5倍異なるのでした。
等級が2異なると、明るさは(1001/5)2倍、すなわち 1002/5倍異なります。
同様に考えると、等級が x異なる場合、明るさは 100x/5異なることになります。
1等星と 6等星の等級の違いは 6-1 = 5等級になり、明るさの違いは 1005/5 = 1001 = 100倍となってちゃんと定義通りになっています。
ここで、星1と星2の明るさを比較することを考えます。
星1からのフラックスをF1、星2からのフラックスをF2とします。
このフラックスというのは、見かけの明るさに対応するものです。
また、星1の等級をm1等、星2の等級をm2等とします。
この場合、星1と星2の等級差はm2-m1なので、明るさの差は
一方、フラックスからの明るさの比は F1/F2と書くことができるので、
目次:
・見かけの等級
見かけの等級とは
見かけの等級の比較 - ポグソンの式
見かけの等級の値
・絶対等級
絶対等級とは
パーセク
絶対等級と見かけの等級の関係式
・等級の計算例
見かけの等級
見かけの等級とは
見かけの等級の比較 - ポグソンの式
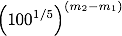 となります。
これは書き換えると
となります。
これは書き換えると
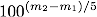 となります。
となります。
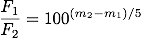
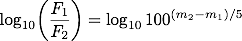
対数の指数と係数のルールより、対数をとった式の右辺は、
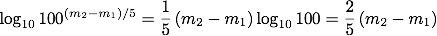
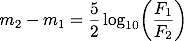
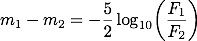
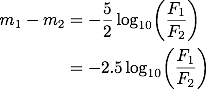
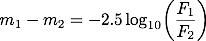
この関係式は、しばしばポグソンの式と呼ばれます。 表記には揺れがあるようで、ポグソンの公式、ポグソンの方程式、ポグソンの法則などと書かれているものもありますが、どれも指しているものは同じです。 理科年表では「ポグソンの式」と表記されていますが、インターネット上での検索では「ポグソンの公式」の方が多くヒットするようです。 ポグソンによって導入されたこの式を用いることによって、等級は天体の明るさを表す定量的な指標となりました。
上記の式は、右辺の対数部分を分解して
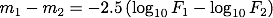
見かけの等級の値
ポグソンの式の導入によって等級の概念は曖昧なものでは無くなりました。 しかし上記のポグソンの式のみでは、2つの天体の等級の差 (m1-m2)は決まりますが、ある特定の天体の見かけの等級の値を決定することは出来ていません。
等級の値を決めるには、何らかの基準が必要です。 そこで、(見かけの)等級の基準となる星を選び、その等級をm0と定めます。 また、その星の明るさ(フラックス)の測定値をF0とします。 この基準の星と比較した場合、星1と基準の星の等級差は
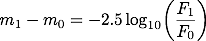
こうなると、基準の星をどうするかが重要になって来ます。 ポグソンが 1856年に等級の定義を定めた際は、北極星の見かけの等級をちょうど 2と定め、北極星を基準に等級を決定していました。 つまり、F0には北極星の明るさ(フラックス)、m0には 2が入り、ある星からのフラックスF1の測定値を代入することによってその星の等級m1が計算出来ます。
しかしその後、北極星は変光星であることが判明しました。 北極星が変光星の可能性があるという疑いは 1852年ごろに出ていましたが、間違いなく変光星であるという事実はアイナー・ヘルツシュプルング (Ejnar Hertzsprung)によって 1911年に明らかにされました。 現在では、ケフェイド変光星というタイプの変光星であることがわかっています。 北極星の変更度合いは時期によって異なり、1963年以前の観測では等級にして 0.1の振幅を持つ変動があり、またそれは徐々に小さくなっていました。 1966年以降に変更幅は急速に小さくなり、現在までに多少の変動はありつつ 0.05等級の振幅で変動をしています。
いずれにせよ、光度に変動がある恒星を明るさの基準として用いるのは都合が悪いため、北極星は等級を評価する際の基準としては使われなくなりました。 その後は、こぐま座ラムダ星を 6.5等と定義するもの、北極星付近の96個の恒星を基準として等級を定めるものなど、複数の定義の変遷がありました。 現在の等級の基準は 1953年に定められたもので、複数の恒星を特定の波長のフィルターを通して測光した場合の平均値を元に定められています。
また業界によって異なる定義を採用している場合もあり、例えば赤外線領域での観測の際には別の定義が多く用いられています。
とにかく、現在はある特定の恒星を等級の基準として扱うのではなく、複数の波長域で複数の標準星となる恒星の観測値を元にして等級の原点が決定されているという点においては同じです。
実際の測光の際には、定義にある複数の基準星と、明るさを比較したい観測対象の天体が同一視野に見えるという保証はないため、測定の為の二次標準星も多数存在します。
天体の見かけの明るさの指標として見かけの等級の概念が導入され、定量的な評価方法としてポグソンの考案した定義が用いられているのは上で紹介した通りです。
見かけの等級では、その天体の本来放っている光量やその天体までの距離などの要素は考えず、単純に地球から見た時の明るさを評価していました。
しかし、地球から天体までの距離によらない明るさの比較をしたい場合は、天体までの距離と天体の明るさの違いが混ざり合った値である見かけの等級をそのまま使うことはできません。
そこで使われるのが絶対等級 (absolute magnitude)です。
天体の絶対等級の定義は、天体を 10 pcの距離から見た時の等級です。
pc (パーセク, parsec)については後で紹介します。
つまり、天体を 10 pcという基準の距離だけ離れて見た場合に、その天体の等級の値はどうなるかを比較して、恒星本来の明るさを評価しようという指標です。
見かけの等級の場合は、近くにいるため明るい(等級は小さい)のか、天体自体が明るいため明るいのかの区別は出来ませんでしたが、絶対等級の場合は基準の距離を定めて比較する指標であるため、距離による明るさの変化とは関係のない値となります。
ここで pc (パーセク, parsec)は天文学で頻繁に用いられる距離の単位であり、
ずいぶんと中途半端な値だと思うかもしれませんが、パーセクにもちゃんとした定義があります。
それは、年周視差が1秒角となるような距離を 1 pcと定義する、というものです。
年周視差(stellar parallax, annual parallax)とは、地球の公転による位置変化によって天体の見かけの位置が変化する事や、あるいはその変化量です。
変化量は角度で表しますが、年周視差は非常に小さく、度を用いて表すのは不便であるため、度の 3600分の1である秒を用います。
時間の秒との混同を避けるため秒角と表す事もあります。
年周視差の角度は、地球・太陽・天体の直角三角形を考えたときに、天体が頂点となっている方の角度に相当します。
この角度をθとし、太陽から天体までの距離をdをすると、この直角三角形には以下の関係式が成り立ちます。
この式をdの式に直すと、
絶対等級
絶対等級とは
パーセク
1 pc = 3.26156...光年 = 3.08568..×1016 m
となります。
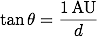
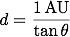
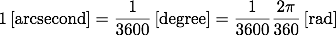
この基準は、視差を意味する"parallax"と、角度の単位でもある秒(あるいは秒角)を意味する"second"から、"parsec"という名前が付けられています。
パーセクは一般にはあまり馴染みの無い距離の単位です。
しかしパーセクは観測と直接結びついた距離の指標であり、年周視差が測定出来る天体までの距離は、年周視差から直接計算することができます。
学術的な場面では距離の単位としては光年よりもパーセクの方が好まれる傾向にあります。
ここでは、天体の見かけの等級とその天体までの距離から、その天体の絶対等級を計算するための関係式を導出します。
ある天体の光度を
絶対等級と見かけの等級の関係式
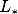 とすると、その天体からrだけ離れた位置でのフラックスは
とすると、その天体からrだけ離れた位置でのフラックスは
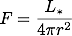
この式から、天体からの距離r1でのフラックスF1は
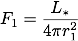
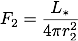
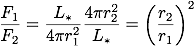
絶対等級の基準になる距離は、天体から 10 pcの距離でした。 そのため、r1 = 10 pcとすると、F1は天体から 10 pc離れた位置でのフラックスを意味します。 また、r2を地球から天体までの距離 d [pc]とすると、F2は地球でのフラックス(地球で観測出来るその天体からのフラックス)になります。 従って、フラックスの比は
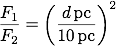
ここで、見かけの等級の違いを表すポグソンの式
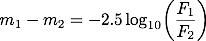
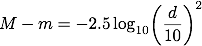
この式の右辺は、以下のように変形出来ます。
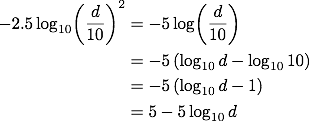
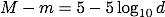
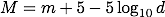
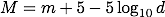
この式を用いて、天体の見かけの等級と、その天体までの距離から絶対等級を計算することができます。
ここでは、見かけの等級と明るさの関係や、絶対等級と距離の関係などについての具体的な計算例を紹介します。
ここまでで計算したように、天体の明るさと等級の間には
等級の計算例
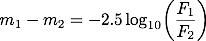 ・・・(1)
・・・(1)
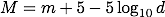 ・・・(2)
・・・(2)ここで、m1 = 1、m2 = 4とします。 1等星の明るさ(フラックス)がF1、4等星の明るさがF2ということになります。 (1)式に代入すると、
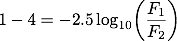
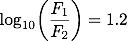
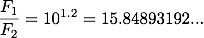
当然ですが、代入する方を逆にしても同じ結果が得られます。 先ほどとは逆に、m1 = 4、m2 = 1としてみます。 この時は、4等星の明るさ(フラックス)がF1、1等星の明るさがF2ということになります。 同様に代入して計算すると、
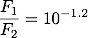
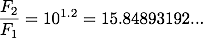
シリウスの等級を m1 = -1.47、北極星の等級を m2 = 2.00とします。 この場合、シリウスの明るさ(フラックス)がF1、北極星の明るさがF2ということになります。 例題 1と同様(1)式に代入して整理すると
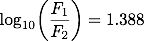
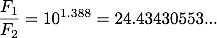
明るい方の星のフラックスをF1、暗い方の星のフラックスをF2とすると、2つの星の明るさが1000倍違うということは F1/F2 = 1000であるということになります。 これを(1)式に代入すると、
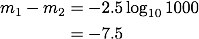
今回の問題では 2つの星の明るさの比しか与えられていないため、等級の差を求めることはできますが、それぞれの等級を求めることは出来ません。
見かけの等級と絶対等級の問題であるため、(2)式を使います。 m = 2.00、d = 100を代入すると、絶対等級 Mは
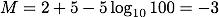
(1) それぞれの星の絶対等級は?
(2) 見かけの等級で比較した場合、どちらが何倍明るいか?
(3) 絶対等級で比較した場合、どちらが何倍明るいか?
(1)
まずはシリウスの絶対等級を求めます。
見かけの等級と距離が分かっているので、(2)式に値を代入すると、
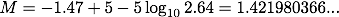
続いてデネブも同様に(2)式に値を代入すると、
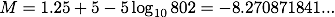
(2)
次に、見かけの等級での明るさを比較します。
シリウスの見かけの等級を m1、デネブの見かけの等級をm2として(1)式に値を代入すると、
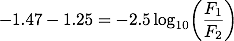
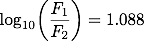
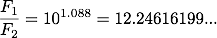
(3)
最後に、絶対等級での明るさを比較します。
ここで扱っているのは絶対等級ですが、等級間の明るさの比較をしたいので(1)を使います。
シリウスの絶対等級を m1、デネブの絶対等級をm2として(1)式に値を代入すると、
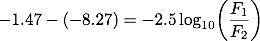
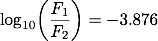
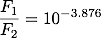
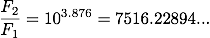
シリウスは夜空で一番明るく見える恒星ですが、これは太陽系に比較的近い位置にあることが主な要因です。 実際の明るさとしてはデネブのように、シリウスの数千倍以上の明るさを持つ恒星も多数存在しますが、太陽系からの距離が離れているために見かけの明るさとしてはシリウスよりも暗いものばかりになります。
太陽と地球の距離は 1 AUです。 見かけの等級と絶対等級の関係であるため(2)式を使うことになりますが、(2)式での距離 dの単位は pcであるため、1 AUを pcに直してやる必要があります。 パーセクの項で扱ったように、1 pc = 206264.8 AUという関係があります。 よって、太陽と地球の距離を pcで表すと、1/206264.8 pcとなることになります。 これを(2)式に代入すると、
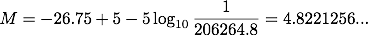
太陽は他の恒星に比べると遥かに近くにあるため見かけの等級は非常に小さな値になりますが、絶対等級に直すとそれほど明るくないことが分かります。
見かけの等級や絶対等級は恒星に限らず、銀河などの天体や、新星や超新星といった突発天体に対しても同じように適用することができます。 まず SN 1987Aについて、(2)式から絶対等級を求めると、
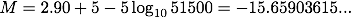
同様に SN 1054の値を代入して計算すると、
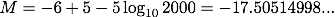
(1) ベテルギウスが SN 1987Aと同程度の超新星を起こした場合、地球からは何等級で見えるか?
(2) ベテルギウスが SN 1054と同程度の超新星を起こした場合、地球からは何等級で見えるか?
(1)
まずは SN 1987Aと同じ明るさの超新星になった場合を考えます。
(2)式において、絶対等級 Mに -15.66、距離 dに 197 pcを代入して、見かけの等級 mを求めれば良いということになります。
それぞれ代入すると、
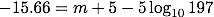
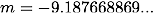
(2)
次に SN 1054と同じ明るさの超新星になった場合を考えます。
同様に(2)式において、絶対等級 Mに -17.51、距離 dに 197 pcを代入すると、
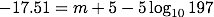
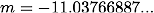
超新星には、超新星を起こした天体の特徴によっていくつか種類がありますが、SN 1987Aと SN 1054は両方ともII型超新星 (type-II supernova)と呼ばれるタイプの超新星だと考えられています(II型の中にもさらに分類はあります)。 両者の絶対等級を比較すると SN 1987Aがやや暗いですが、SN 1987Aは他の同タイプの超新星と比べるとやや暗いことが分かっています。 これは、超新星を起こす直前の恒星が半径が比較的小さい青色超巨星だったことが原因だと考えられています。
一方、ベテルギウスもいずれII型超新星を起こします。 ベテルギウスは大きく膨張した赤色超巨星であるため、SN 1987Aよりは明るい、他の標準的なII型超新星と同程度の明るさになることが期待されます(実際には発生してみないと分からない部分もあります)。 SN 1054と同程度の明るさになった場合は、上での計算の通り、地球から見た時の等級は -11等程度になると予想されています。
参考として、満月の等級は -12.7、半月の時の等級はおよそ -10等です。
従って、-11等というのは半月よりは明るく満月よりは暗い程度ということになります。
しばしば、ベテルギウスが超新星を起こした時の明るさは、半月より明るく満月よりは暗い程度と言われることがありますが、これはこれまでの同じタイプの超新星の絶対等級と、ベテルギウスまでの距離からおおまかに計算することができます。
脚注
10を底とする対数は常用対数 (common logarithm)で、しばしば底の10を省略して log x と表記されます。 常用対数であることを区別する場合は底の10を表記するか、あるいは Log x とLを大文字で書く場合もあります。 一方、e (ネイピア数)を底とする対数 loge x は自然対数 (natural logarithm)と呼ばれ、自然科学では頻出します。 自然対数を log x と底を省略して表記する場合もありますが、常用対数との混同を避けるため、多くの場合は ln x という表記が用いられます。 また、2を底とする対数 log2 x は二進対数 (binary logarithm)と呼ばれます。 二進対数も log x という表記を用いる場合もありますが、同じく混同を避ける為に lb x という表記をする場合があります。参考文献
理科年表2015年7月18日