流体には様々な不安定性が存在します。 例えば、温度勾配や組成勾配がある状況での対流不安定などがその一例です。
ここでは、流体の層の境界面で発達する種類の不安定性と、その不安定性を判別するための条件について紹介します。 流体層の境界面で発生する不安定性の代表例には、レイリー・テイラー不安定性 (Rayleigh-Taylor instability) と、ケルビン・ヘルムホルツ不安定性 (Kelvin–Helmholtz instability) があります。 レイリー・テイラー不安定性は、簡単に言うと、密度の低い (軽い) 流体の上に密度の大きい (重い) 流体が乗っている時に発生する不安定性です。 またケルビン・ヘルムホルツ不安定性は、2 つの密度の異なる流体の層に速度差がある時に発生する不安定性です。
どちらの不安定性も、同じ基礎方程式の線形解析からその性質について考察を行うことが出来ます。
まずは流体の基礎方程式の線形解析を行って分散関係を導出し、得られた分散関係からレイリー・テイラー不安定性とケルビン・ヘルムホルツ不安定性の性質について紹介します。
目次:
関連ページ:
線形不安定性解析
初期条件の設定
線形不安定性解析の初期条件として、\(z\) 軸の負の方向に重力がかかっているという状況を考えます。 つまり、\(z\) 軸の正の方向が「上」、負の方向が「下」という状況です。 また、\(z=0\) を境にして、上下の流体の密度と、水平方向の速度が異なっている、という状態を考えます。 このとき、簡単のために流体の水平方向の速度は \(x\) 成分のみが存在するとします。
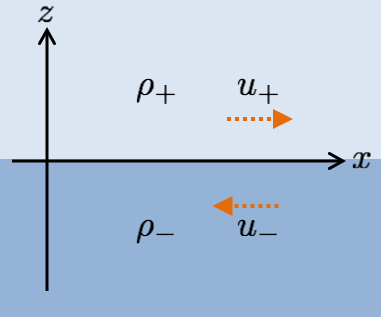
図のように、初期の平衡状態での流体の密度 \(\rho_{0}\) は \begin{align*} \rho_{0}=\left\{ \begin{array}{ll} \rhop & \left(z\geq0\right) \\ \rhom & \left(z\lt0\right) \end{array} \right. \end{align*} とし、速度は \begin{align*} \bm{v_{0}}=\left(v_{x0},\,0,\,0\right)=\left\{ \begin{array}{ll} \left(\up,\,0,\,0\right) & \left(z\geq0\right) \\ \left(\um,\,0,\,0\right) & \left(z\lt0\right) \end{array} \right. \end{align*} とします。 ここで、\(\rhop\)、\(\rhom\)、\(\up\)、\(\um\) はそれぞれ定数とします。 なお、図では \(\up\) と \(\um\) は逆方向に流れているように描いていますが、この段階では上層と下層の速度の大きさや向きは特に問いません。 また上層と下層の密度の大小も現時点では問いません。 \(z=0\) の境界で密度や速度などが不連続であるという条件が重要です。 この状態で、上下層の速度をどちらも 0 として上層の密度のほうが大きいとした場合がレイリー・テイラー不安定性が発達しうる状況、上下層に速度差がある状態がケルビン・ヘルムホルツ不安定性が発達しうる状況におおむね対応します。
ここでは \(z=0\) での不連続を除いて、上層も下層も密度は一定としています。
本来は密度は \(z\) 依存性を持つはずですが、圧力のスケールハイトよりも十分に短い領域を考える場合であれば、密度は変化しないとみなすことが出来ます。
またこのような状況で流体の流れが低速の場合は、流体は非圧縮であると近似することが出来ます。
以下では、流体は非圧縮であり、粘性は働かないものとして線形不安定性解析を行います。
速度に以下のようなゆらぎを与えます。
\begin{align*}
\bm{v}&=\bm{v_{0}}+\left(\delta u,\,0,\,\delta w\right)e^{i\left(kx-\omega t\right)}\\
&=\left(v_{x0}+\delta u\,e^{i\left(kx-\omega t\right)},\,0,\,\delta w\,e^{i\left(kx-\omega t\right)}\right)
\end{align*}
ここで、\(k \gt 0\) はゆらぎの波数、\(\delta u\) と \(\delta w\) はそれぞれ \(x\)、\(z\) 成分の速度の微小ゆらぎで、\(z\) のみの関数とします。
同様に、密度と圧力のゆらぎも以下のように与えます。
\begin{align*}
\rho=\rho_{0}+\delta\rho\,e^{i\left(kx-\omega t\right)}
\end{align*}
\begin{align*}
p=p_{0}+\delta p\,e^{i\left(kx-\omega t\right)}
\end{align*}
線形不安定性解析
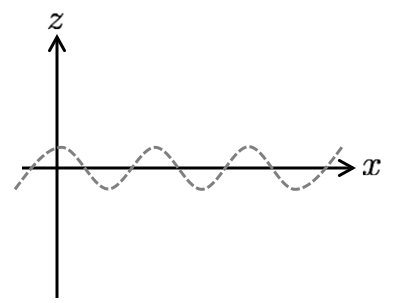
これは、2 つの流体層の境界面 \(z=0\) において、各物理量に対して \(x\) 軸方向に波数 \(k\) の微小な波を与えた事に対応します。 この微小なゆらぎを流体の基礎方程式に代入して \(\omega\) と波数 \(k\) の関係 (分散関係) を導出することによって、与えたゆらぎの波数によってそのゆらぎがどのように成長するか (あるいは減衰するか) を調べます。 微小な揺らぎが成長する場合はその系は不安定、振動したり減衰したりする場合はその系は安定です。
流体の運動方程式
流体の運動方程式は以下のように表せます。 \begin{align*} \frac{\del\bm{v}}{\del t}+\left(\bm{v}\cdot\nabla\right)\bm{v}+\frac{1}{\rho}\nabla p=\bm{g} \end{align*} \(\bm{g}\) は重力の項で、\(\bm{g}=\left(0,\,0,\,-g\right)\) となります。 上記の通り、粘性項は無視しています。 両辺に \(\rho\) をかけると、 \begin{align} \rho\frac{\del\bm{v}}{\del t}+\rho\left(\bm{v}\cdot\nabla\right)\bm{v}+\nabla p=\rho\bm{g} \label{eom} \end{align} となります。 この式に \(\bm{v}\)、\(\rho\)、\(p\) を代入し、1 次の微小量だけを残します (微小量の 2 次の項は非常に小さくなるため無視します)。 例えば、式 \eqref{eom} の左辺第 1 項の \(x\) 成分は、 \begin{align*} \left.\rho\frac{\del\bm{v}}{\del t}\right|_{x} &= \left(\rho_{0}+\delta\rho\,e^{i\left(kx-\omega t\right)}\right)\frac{\del}{\del t}\left(v_{x0}+\delta u\,e^{i\left(kx-\omega t\right)}\right)\\ &=\left(\rho_{0}+\delta\rho\,e^{i\left(kx-\omega t\right)}\right)\left(-i\omega\delta u\,e^{i\left(kx-\omega t\right)}\right)\\ &=-i\omega\rho_{0}\delta u\,e^{i\left(kx-\omega t\right)} \end{align*} となります。 途中で \(\delta\rho\delta u\) の項が出てきますが、この項は微小量同士の積になっているため 2 行目から 3 行目に移る時に落としています。 同様に、第 2 項に関しては、 \begin{align*} \left.\left(\bm{v}\cdot\nabla\right)\bm{v}\right|_{x} &= \left(v_{x0}+\delta u\,e^{i\left(kx-\omega t\right)},0,\,\delta w\,e^{i\left(kx-\omega t\right)}\right)\cdot\left(\frac{\del}{\del x},\,\frac{\del}{\del y},\,\frac{\del}{\del z}\right)\left(v_{x0}+\delta u\,e^{i\left(kx-\omega t\right)}\right)\\ &=\left(v_{0x}+\delta u\,e^{i\left(kx-\omega t\right)}\right)\frac{\del}{\del x}\left(v_{0x}+\delta u\,e^{i\left(kx-\omega t\right)}\right)+\delta w\,e^{i\left(kx-\omega t\right)}\frac{\del}{\del z}\left(v_{0x}+\delta u\,e^{i\left(kx-\omega t\right)}\right)\\ &=\left(v_{0x}\delta u\,e^{i\left(kx-\omega t\right)}\right)\left(ik\delta u\,e^{i\left(kx-\omega t\right)}\right)+\delta w\,e^{i\left(kx-\omega t\right)}\left(\frac{d}{dz}\delta u\right)e^{i\left(kx-\omega t\right)}\\ &=ikv_{x0}\delta u\,e^{i\left(kx-\omega t\right)} \end{align*} となるため、 \begin{align*} \left.\rho\left(\bm{v}\cdot\nabla\right)\bm{v}\right|_{x} &= \left(\rho_{0}\delta\rho\,e^{i\left(kx-\omega t\right)}\right)\left(ikv_{x0}\delta u\,e^{i\left(kx-\omega t\right)}\right)\\ &=i\rho_{0}kv_{x0}\delta u\,e^{i\left(kx-\omega t\right)} \end{align*} となります。 また、圧力勾配項の \(x\) 成分は、 \begin{align*} \left.\nabla p\right|_{x}=\frac{\del}{\del x}\left(p_{0}+\delta p\,e^{i\left(kx-\omega t\right)}\right)=ik\delta p\,e^{i\left(kx-\omega t\right)} \end{align*} になります。 圧力は \(x\) 方向には一様であるという状況を考えているため、\(p_{0}\) や \(\delta p\) の \(x\) 微分は 0 になります。
従ってこれらをまとめると、運動方程式 \eqref{eom} の \(x\) 成分は \begin{align*} i\rho_{0}\left(-\omega+kv_{x0}\right)\delta u+ik\delta p=0 \end{align*} となります。
同様にして、運動方程式の \(z\) 成分も計算します。 式 \eqref{eom} の左辺第 1 項の \(z\) 成分は、 \begin{align*} \left.\rho\frac{\del\bm{v}}{\del t}\right|_{z} &= \left(\rho_{0}+\delta\rho\,e^{i\left(kx-\omega t\right)}\right)\frac{\del}{\del t}\left(\delta w\,e^{i\left(kx-\omega t\right)}\right)\\ &=\left(\rho_{0}+\delta\rho\,e^{i\left(kx-\omega t\right)}\right)\left(-i\omega\delta w\,e^{i\left(kx-\omega t\right)}\right)\\ &=-i\omega\rho_{0}\delta w\,e^{i\left(kx-\omega t\right)} \end{align*} であり、 \begin{align*} \left.\left(\bm{v}\cdot\nabla\right)\bm{v}\right|_{z} &= \left(v_{x0}+\delta u\,e^{i\left(kx-\omega t\right)},\,0,\,\delta w\,e^{i\left(kx-\omega t\right)}\right)\cdot\left(\frac{\del}{\del x},\,\frac{\del}{\del y},\,\frac{\del}{\del z}\right)\left(\delta w\,e^{i\left(kx-\omega t\right)}\right)\\ &=\left(v_{x0}+\delta u\,e^{i\left(kx-\omega t\right)}\right)\frac{\del}{\del x}\left(\delta w\,e^{i\left(kx-\omega t\right)}\right)+\delta w\,e^{i\left(kx-\omega t\right)}\frac{\del}{\del z}\left(\delta w\,e^{i\left(kx-\omega t\right)}\right)\\ &=\left(v_{0x}+\delta u\,e^{i\left(kx-\omega t\right)}\right)\left(ik\delta w\,e^{i\left(kx-\omega t\right)}\right)+\delta w\,e^{i\left(kx-\omega t\right)}\left(\frac{d}{dz}\delta w\right)\,e^{i\left(kx-\omega t\right)}\\ &=ikv_{x0}\delta w\,e^{i\left(kx-\omega t\right)} \end{align*} となるため、式 \eqref{eom} の左辺第 2 項の \(z\) 成分は、 \begin{align*} \left.\rho\left(\bm{v}\cdot\nabla\right)\bm{v}\right|_{z} &= \left(\rho_{0}+\delta\rho\,e^{i\left(kx-\omega t\right)}\right)\left(ikv_{x0}\delta w\,e^{i\left(kx-\omega t\right)}\right)\\ &=i\rho_{0}kv_{x0}\delta w\,e^{i\left(kx-\omega t\right)} \end{align*} となります。 また、圧力勾配項の \(z\) 成分は、 \begin{align*} \left.\nabla p\right|_{z}&=\frac{\del}{\del z}\left(p_{0}+\delta p\,e^{i\left(kx-\omega t\right)}\right)\\ &=\frac{dp_{0}}{dz}+e^{i\left(kx-\omega t\right)}\frac{d}{dz}\delta p \end{align*} となります。 ここで、\(\delta p\) などの微小量は \(z\) の関数であることに注意します。 さらに重力の項は \begin{align*} \left.\rho\bm{g}\right|_{z}&=\left(\rho_{0}+\delta\rho\,e^{i\left(kx-\omega t\right)}\right)\left(-g\right)\\ &=-\rho_{0}g-\delta\rho g\,e^{i\left(kx-\omega t\right)} \end{align*} となります。 以上をまとめると,運動方程式 \eqref{eom} の \(z\) 成分は \begin{align*} i\rho_{0}\left(-\omega+kv_{x0}\right)\delta w\,e^{i\left(kx-\omega t\right)}+\frac{d\rho_{0}}{dz}+\frac{d}{dz}\delta p\,e^{i\left(kx-\omega t\right)}+\rho_{0}g+\delta\rho g\,e^{i\left(kx-\omega t\right)}=0 \end{align*} と書けます。
一方、平衡状態においては静水圧平衡 \begin{align*} \frac{dp_{0}}{dz}=-\rho g \end{align*} が成立するため、これを用いると \begin{align*} i\rho_{0}\left(-\omega+kv_{x0}\right)\delta w+\frac{d}{dz}\delta p+\delta\rho g=0 \end{align*} とまとめることができます。
以上より、運動方程式 \eqref{eom} の 1 次の微小量だけを残した式は、\(x\) 成分と \(z\) 成分がそれぞれ \begin{align} i\rho_{0}\left(-\omega+kv_{x0}\right)\delta u+ik\delta p&=0 \label{eomx}\\ i\rho_{0}\left(-\omega+kv_{x0}\right)\delta w+\frac{d}{dz}\delta p+\delta\rho g&=0 \label{eomz} \end{align} となります。 なお、\(y\) 成分は全て 0 となります。
連続の式
ここでは流体は非圧縮性であることを仮定しています。 非圧縮流体の条件は、 \begin{align*} \nabla\cdot\bm{v}=0 \end{align*} です。 この式に \(\bm{v}\) を代入すると、左辺は \begin{align*} \nabla\cdot\bm{v}&=\left(\frac{\del}{\del x},\,\frac{\del}{\del y},\,\frac{\del}{\del z}\right)\cdot\left(v_{x0}+\delta u\,e^{i\left(kx-\omega t\right)},\,0,\,\delta w\,e^{i\left(kx-\omega t\right)}\right)\\ &=ik\delta u\,e^{i\left(kx-\omega t\right)}+\frac{d}{dz}\delta w\,e^{i\left(kx-\omega t\right)} \end{align*} となるため、 \begin{align} ik\delta u+\frac{d}{dz}\delta w=0 \label{incomp} \end{align} が得られます。
一方、流体の質量保存則 (連続の式) は、以下のように書けます。 \begin{align*} \frac{\del\rho}{\del t}+\nabla\cdot\left(\rho\bm{v}\right)=0 \end{align*}
この式に \(\rho\) と \(\bm{v}\) を代入すると、左辺は \begin{align*} \frac{\del\rho}{\del t}+\nabla\cdot\left(\rho\bm{v}\right) &= \frac{\del}{\del t}\left(\rho_{0}+\delta\rho\,e^{i\left(kx-\omega t\right)}\right)\\ \qquad&+\frac{\del}{\del x}\left\{\left(\rho_{0}+\delta\rho\,e^{i\left(kx-\omega t\right)}\right)\left(v_{x0}+\delta u\,e^{i\left(kx-\omega t\right)}\right)\right\}+\frac{\del}{\del z}\left\{\left(\rho_{0}+\delta\rho\,e^{i\left(kx-\omega t\right)}\right)\delta w\,e^{i\left(kx-\omega t\right)}\right\}\\ &=\left(-i\omega\delta\rho+ik\rho_{0}\delta u+ikv_{x0}\delta p+\delta w\frac{d\rho_{0}}{dz}+\rho_{0}\frac{d}{dz}\delta w\right)e^{i\left(kx-\omega t\right)} \end{align*} となるので、 \begin{align*} -i\omega\delta\rho+ik\rho_{0}\delta u+ikv_{x0}\delta p+\delta w\frac{d\rho_{0}}{dz}+\rho_{0}\frac{d}{dz}\delta w = 0 \end{align*} を得ます。 この式に、非圧縮の条件である式 \eqref{incomp} を代入して整理すると、 \begin{align} \left(-i\omega+ikv_{x0}\right)\delta\rho+\delta w\frac{d\rho_{0}}{dz}=0 \label{cont} \end{align} を得ます。
ここでは、上層と下層の境界である \(z=0\) の部分を除くと、密度は一様であると仮定しています。 従って、\(z\neq0\) では \(\displaystyle{\frac{d\rho_{0}}{dz}=0}\) となります。 これを式 \eqref{cont} に代入すると、\(z\neq0\) では \begin{align*} \delta\rho=0 \end{align*} であるということが分かります。 これは、\(z=0\) の境界以外の領域では、密度揺らぎは 0 であるということを意味しています。
境界面以外での振る舞い
まずは、ゆらぎを与えている境界面以外の領域での振る舞いを調べます。 式 \eqref{eomx}、\eqref{eomz}、\eqref{incomp} の 3 式に \(\delta\rho=0\) を代入すると、以下の 3 式を得ます。 \begin{align} i\rho_{0}\left(-\omega+kv_{x0}\right)\delta u+ik\delta p&=0 \label{eomx2} \\ i\rho_{0}\left(-\omega+kv_{x0}\right)\delta w+\frac{d}{dz}\delta p&=0 \label{eomz2} \\ ik\delta u+\frac{d}{dz}\delta w&=0 \label{incomp2} \end{align} この 3 式から、\(\delta p\)、\(\delta u\)、\(\delta w\) についての式を導出します。
まず式 \eqref{eomz2} の両辺を \(z\) で微分すると、 \begin{align*} \frac{d^{2}}{dz^{2}}\delta p=-i\rho_{0}\left(-\omega+kv_{x0}\right)\frac{d}{dz}\delta w \end{align*} となるため、これに式 \eqref{incomp2} を代入すると \begin{align*} \frac{d^{2}}{dz^{2}}\delta p=-i\rho_{0}\left(-\omega+kv_{x0}\right)\delta u \end{align*} となります。 さらに式 \eqref{eomx2} を代入して \(\delta u\) を消去すると、 \begin{align*} \frac{d^{2}}{dz^{2}}\delta p=k^{2}\delta p \end{align*} が得られます。 同様に \(\delta u\) と \(\delta w\) についても求めて 3 式をまとめて書くと、 \begin{align} \frac{d^{2}}{dz^{2}}\left(\delta p,\,\delta u,\,\delta w\right)=k^{2}\left(\delta p,\,\delta u,\,\delta w\right) \label{d2dz2} \end{align} となります。
この式は \begin{align*} \frac{d^{2}f\!\left(z\right)}{dz^{2}}=k^{2}f\!\left(z\right) \end{align*} という \(z\) についての 2 階微分方程式になっています。 この形の微分方程式の一般解は、積分定数を \(A\)、\(B\) として \begin{align*} f\!\left(z\right)=Ae^{kz}+Be^{-kz} \end{align*} と書くことが出来ます。
ここで、2 層の境界から十分離れた遠方ではゆらぎが小さいという条件を用います。 \(z\gt0\) では \(e^{-kz}\) に比例する解、\(z\lt0\) では \(e^{kz}\) に比例する解を持てば、ゆらぎは両方の無限遠で 0 になる会となります。 従って、式 \eqref{d2dz2} の解は、 \begin{align} \left(\delta p,\,\delta u,\,\delta w\right)=\left\{ \begin{array}{ll} \left(\delta\pp,\,\delta\up,\,\delta\wpl\right)e^{-kz} & \left(z\gt0\right)\\ \left(\delta\pmi,\,\delta\um,\,\delta\wm\right)e^{kz} & \left(z\lt0\right) \end{array} \right. \label{sol} \end{align} と書くことが出来ます。 ここで、\(+\) と \(-\) の添字は、それぞれ境界 \(z=0\) のすぐ上とすぐ下での値であることを表します。
境界面での連続条件
2 層の境界では、\(\delta\wpl\) と \(\delta\wm\) などの物理量は境界面を挟んで不連続になっています。 そこで、境界面において流体素片が満たす方程式から、境界面における連続条件を導出します。
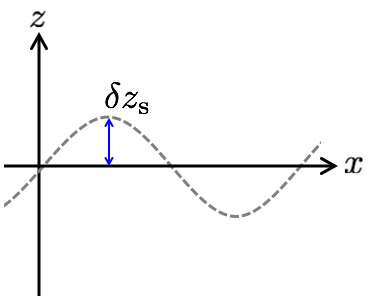
図のように、与えたゆらぎによる境界面からの微小な変動の大きさを \(\delta\zs\) とします。 この微小変化 \(\delta\zs\) に沿った時間変動が、\(z\) 方向の速度ゆらぎ \(\delta\ws\) となるため、以下のように書くことが出来ます。 \begin{align} \frac{d}{dt}\delta\zs=\delta\ws \label{deltazs} \end{align} 添字の \({\rm s}\) は境界面での値であることを示します。 また他のゆらぎと同様に、\(\delta\zs\) も \(e^{i\left(kx-\omega t\right)}\) に比例します。 式 \eqref{deltazs} の左辺は \begin{align*} \frac{d}{dt}\delta\zs&=\frac{\del}{\del t}\delta\zs+v_{x0}\frac{\del}{\del x}\delta\zs\\ &=-i\omega\delta\zs+ikv_{x0}\delta\zs \end{align*} となるので、 \begin{align*} \delta\zs=\frac{i\delta\ws}{\omega-kv_{x0}} \end{align*} という関係式が得られます。 上層の \(z\gt0\) と下層 \(z\lt0\) での値をそれぞれ考えると、 \begin{align} \delta\zs=\frac{i\delta\wpl}{\omega-k\up}=\frac{i\delta\wm}{\omega-k\um} \label{boundary} \end{align} となることが分かります。 従って、上層と下層の境界における連続条件は、 \begin{align*} \frac{\delta\wpl}{\omega-k\up}=\frac{\delta\wm}{\omega-k\um} \end{align*} となります。 境界面では \(\delta\wpl\) と \(\delta\wm\) は不連続ですが、この量は連続になっているということを表します。
境界面前後での基礎方程式
ここで、境界面における式 \eqref{cont} を考えます。 境界面以外では \(\displaystyle{\frac{d\rho_{0}}{dz}=0}\) となりましたが、境界面においては密度の変化があるため \(\displaystyle{\frac{d\rho_{0}}{dz}\neq0}\) です。 式 \eqref{cont} から、式 \eqref{boundary} を用いて \(\delta w\) を消去すると、 \begin{align} \delta\rho=-\frac{d\rho_{0}}{dz}\delta\zs \label{deltarho} \end{align} が得られます。 境界面では異なる密度の流体が接しているため、密度に飛びがあることになります。 そのため境界面での密度勾配 \(\displaystyle{\frac{d\rho_{0}}{dz}}\) は発散し、左辺の \(\delta\rho\) も発散することになります。
発散してしまう量はそのままでは扱いづらいので、境界面を含むごく狭い領域 \(\left(-\epsilon\leq z \lt \epsilon\right)\) で積分することで取り扱いやすくします。 式 \eqref{deltarho} の両辺を境界面を含むごく狭い領域で積分すると、 \begin{align} \int_{-\epsilon}^{\epsilon}\delta\rho\,dz=-\left(\rhop-\rhom\right)\delta\zs \label{integral} \end{align} となります。
式 \eqref{eomz} を同じ範囲で積分します。 第 1 項は発散する項が含まれていないため、境界を挟んだごく狭い領域での積分を行った結果は無視できるほど小さい値となります。 一方で第 2 項と 第 3 項は、境界面で発散する項を含みます。 第 2 項は \begin{align*} \int_{-\epsilon}^{\epsilon}\frac{d}{dz}\delta p\,dz=\delta\pp-\delta\pmi \end{align*} となり、第 3 項は式 \eqref{integral} を用いると \begin{align*} g\int_{-\epsilon}^{\epsilon}\delta\rho\,dz=-g\left(\rhop-\rhom\right)\delta\zs \end{align*} となります。 そのため、式 \eqref{eomz} を境界面を含むごく狭い範囲で積分した結果は、 \begin{align} \delta\pp-\delta\pmi-g\left(\rhop-\rhom\right)\delta\zs=0 \label{eomz3} \end{align} となります。
次に、式 \eqref{eomz} を、\(z\gt0\) と \(z\lt0\) それぞれの領域で考えます。 \(z\gt0\) では、\(\rho_{0}=\rhop\)、\(v_{x0}=\up\)、\(\delta w=\delta\wpl e^{-kz}\) であり、また境界以外の領域であるため \(\delta\rho=0\) となります。 また式 \eqref{sol} より、 \begin{align*} \frac{d}{dz}\delta p=\frac{d}{dz}\delta\pp e^{-kz}=-k\delta\pp \end{align*} となるため、\(z\gt0\) での 式 \eqref{eomz} は \begin{align} i\rhop\left(-\omega+k\up\right)\delta\wpl-k\delta\pp=0 \label{eomzp} \end{align} となります。 同様の議論から、\(z\lt0\) での 式 \eqref{eomz} は \begin{align} i\rhom\left(-\omega+k\um\right)\delta\wm+k\delta\pmi=0 \label{eomzm} \end{align} となります。
分散関係の導出
ここまでに得た式から、分散関係を導出します。
式 \eqref{boundary}、\eqref{eomz3}、\eqref{eomzp}、\eqref{eomzm} の 4 式から \(\delta\wpl\)、\(\delta\wm\)、\(\delta\pp\)、\(\delta\pmi\) を消去して \(\delta\zs\) の式にすると、 \begin{align*} \left\{\rhop\left(-\omega+k\up\right)^{2}+\rhom\left(\omega+k\um\right)^{2}+gk\left(\rhop-\rhom\right)\right\}\delta\zs=0 \end{align*} を得ます。 この方程式の自明な解は \(\delta\zs=0\) というものです。 この方程式が自明でない解 (\(\delta\zs=0\) ではない解) を持つための条件は、\(\delta\zs\) の係数が 0 になることです。 すなわち \begin{align*} \rhop\left(-\omega+k\up\right)^{2}+\rhom\left(\omega+k\um\right)^{2}+gk\left(\rhop-\rhom\right)=0 \end{align*} ということになります。
この式を \(\omega\) について整理すると、 \begin{align*} \omega^{2}-2k\frac{\rhop\up+\rhom\um}{\rhop+\rhom}\omega+k^{2}\frac{\rhop\up^{2}+\rhom\um^{2}}{\rhop+\rhom}+gk\frac{\rhop\rhom}{\rhop+\rhom}=0 \end{align*} となります。 この式は \(\omega\) についての 2 次方程式であり、これを解くことによって今考えている系での線形不安定性解析の分散関係を得ることが出来ます。
いま、ゆらぎは \(e^{i\left(kx-\omega t\right)}\) に比例する形で与えています。
そのため、根号の中が正の場合には、与えたゆらぎが時間とともに指数関数的に成長する解を持つ、つまり不安定であるということになります。
従って不安定条件は、
\begin{align*}
\frac{k^{2}\rhop\rhom}{\left(\rhop+\rhom\right)^{2}}\left(\up-\um\right)^{2}+gk\frac{\rhop-\rhom}{\rhop+\rhom}\gt0
\end{align*}
となりますが、波数 \(k\gt0\) であるため、この不安定条件は
\begin{align*}
\frac{k\rhop\rhom}{\left(\rhop+\rhom\right)^{2}}\left(\up-\um\right)^{2}+g\frac{\rhop-\rhom}{\rhop+\rhom}\gt0
\end{align*}
と書くことが出来ます。
そのため、波数 \(k\) が十分に大きい場合は、\(\up=\um\)、つまり上層と下層の速度差が無い状況でない限り、系は不安定になります。
式 \eqref{disp} で導出した分散関係から、まずはレイリー・テイラー不安定性について考察します。
上下の 2 層の速度が 0 の状況、つまり \(\up=\um=0\) の状態を考えます。
レイリー・テイラー不安定性
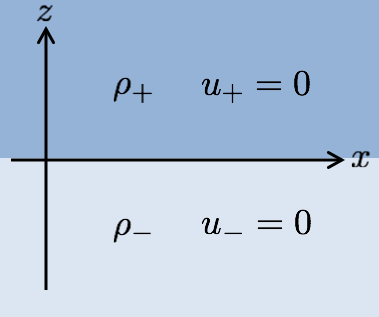
分散関係の式 \eqref{disp} に \(\up=\um=0\) を代入すると、この状況での分散関係は \begin{align} \omega=\pm i\sqrt{gk\frac{\rhop-\rhom}{\rhop+\rhom}} \label{disprt} \end{align} となります。 式 \eqref{disprt} の根号の中が正の場合は \(\omega\) が純虚数になるため、ゆらぎ \(e^{i\left(kx-\omega t\right)}\) は時刻 \(t\) の増加とともに指数関数的に成長するモードが存在し,不安定になります。 逆に根号の中が負であれば \(\omega\) は実数となるため、ゆらぎは振動解となって安定になります。
式 \eqref{disprt} より、系が不安定になる条件は \begin{align*} \rhop-\rhom \gt 0 \end{align*} であることが分かります。 つまり、\(\rhop \gt \rhom\) が不安定になる条件ということです。 これは、低密度の流体 (軽い流体) の上に高密度の流体 (思い流体) が乗っている状況では、2 層の境界面での微小な揺らぎは波数 \(k\) に関わらず (つまりどんな波長のゆらぎに対しても) 指数関数的に成長して不安定となるということをを表しています。 逆に、\(\rhop \lt \rhom\)、つまり高密度の流体の上に低密度の流体が存在する状況では、どんな波数の (どんな波長の) ゆらぎであっても、レイリー・テイラー不安定性に対して安定であるということが分かります。
なおレイリー・テイラー不安定の場合、与えたゆらぎの成長のタイムスケールは \(t_{\rm RT}\sim 1/\omega\) で与えられます。 波長 \(\lambda\) と波数 \(k\) の関係は \begin{align*} \lambda=\frac{2\pi}{k} \end{align*} となるため、成長のタイムスケールは \begin{align*} t_{\rm RT}\sim\frac{1}{\omega}\propto k^{-1/2}\propto\lambda^{1/2} \end{align*} となります。 成長のタイムスケールが短いということは、ゆらぎの成長が速いということを意味します。 つまり、レイリー・テイラー不安定では、ゆらぎの波長が短いほど (= 波数が大きいほど) 早く成長して不安定になります。
- \(\rhop \gt \rhom\) のとき、ゆらぎの波長によらず不安定 (レイリー・テイラー不安定)
- このとき、波長の短いゆらぎほど速く成長する。
- \(\rhop \lt \rhom\) のとき、ゆらぎの波長によらず安定
レイリー・テイラー不安定性の解析では、軽い流体の上に重い流体が乗っている時は境界面で与えるゆらぎの波長によらず必ず不安定、逆に重い流体の上に軽い流体が乗っている場合は波長によらず必ず安定、ということが分かりました。 ただし、ここでは条件を非常に簡単化してあるため、この安定・不安定の条件は必ずしも現実に即してはいません。 例えば上層と下層の境界面における表面張力を考慮した際は、表面張力による安定化作用が加わるため条件は変わります。 表面張力を考慮した場合の条件については後ほど紹介します。
2 層の流れがあるが速度差が 0 の場合
レイリー・テイラー不安定性では、上層と下層の速度はどちらも 0 の状態で、2 層に密度差が存在するという状況を考えました。 上層と下層は水平方向に動いているものの、速度差が 0 という状況を考えると、\(\up=\um=u\left(\neq0\right)\) として分散関係 \eqref{disp} は以下のようになります。 \begin{align*} \omega=ku\pm i\sqrt{gk\frac{\rhop-\rhom}{\rhop+\rhom}} \end{align*}
安定・不安定の条件は、同じく根号の中の正負で決まり、これは式 \eqref{disprt} での条件と同一です。
これは、単に 2 層の流れに乗った座標で見れば、上層も下層も静止しているとみなせることに対応しています。
また、ゆらぎの位相速度は \(\omega/k\) の実部で与えられます。
つまりこれは、ゆらぎが流体の速度に乗って速度 \(u\) で境界面を流れているという状況に対応しています。
次に、式 \eqref{disp} の分散関係から、ケルビン・ヘルムホルツ不安定性について考察します。
ここでは、上下の 2 層の速度が 0 では無い状態を考えます。
ケルビン・ヘルムホルツ不安定性

分散関係 \eqref{disp} からの不安定条件は \begin{align*} \frac{k\rhop\rhom}{\left(\rhop+\rhom\right)^{2}}\left(\up-\um\right)^{2}+g\frac{\rhop-\rhom}{\rhop+\rhom}\gt0 \end{align*} となりますが、\(\rhop+\rhom \gt0\) であることから、 \begin{align} \frac{k\rhop\rhom}{\rhop+\rhom}\left(\up-\um\right)^{2}+g\left(\rhop-\rhom\right)\gt0 \label{dispkh} \end{align} と書き直すことが出来ます。
式 \eqref{dispkh} の左辺第 1 項は正の値になります。 そのため、レイリー・テイラー不安定性に対して不安定な場合、すなわち \(\rhop\gt\rhom\) を満たす場合は、式 \eqref{dispkh} は波数 \(k\) によらず常に成り立ちます。 従って、軽い流体の上に重い流体が乗っているというレイリー・テイラー不安定の状態は、ケルビン・ヘルムホルツ不安定でもあるということになります。
次に、レイリー・テイラー不安定性に対して安定の場合を考えます。 レイリー・テイラー不安定性に対して安定ということは、\(\rhop\lt\rhom\) という条件を満たしているということです。 ここで式 \eqref{dispkh} を変形すると、 \begin{align*} k\gt\frac{g\left(\rhop+\rhom\right)\left(\rhom-\rhop\right)}{\rhop\rhom\left(\up-\um\right)^{2}}\equiv\kcrit \end{align*} となります。 つまり、レイリー・テイラー不安定性に対しては安定である場合であっても、ある臨界波数 \(\kcrit\) よりも大きな波数に対しては必ず不安定になるということを表しています。 波数を波長に書き直すと、 \begin{align} \lambda\lt\frac{2\pi\rhop\rhom\left(\up-\um\right)^{2}}{g\left(\rhop+\rhom\right)\left(\rhom-\rhop\right)}\equiv\lambdacrit \label{dispkh2} \end{align} となります。
従って、重い流体の上に軽い流体が乗っているというレイリー・テイラー不安定性に対して安定な状況であっても、2 層に速度差が存在すると、ある臨界波長 \(\lambdacrit\) よりも短い波長では必ずゆらぎは不安定になるという事が分かります。 このように、2 層の間に速度差が存在することによって境界面で発生する不安定性がケルビン・ヘルムホルツ不安定性です。
式 \eqref{dispkh2} から、ケルビン・ヘルムホルツ不安定性のいくつかの特徴を読み取ることが出来ます。 例えば、2 層の速度差が大きくなると臨界波長 \(\lambdacrit\) も大きくなります。 そのため、速度差が小さいうちは長波長のゆらぎに対しては安定ですが、速度差が大きくなるにつれ、より長波長のゆらぎに対しても不安定となります。 また、上層と下層の密度差が大きい (この場合は、下層がより重く、上層はより軽い) 場合は、臨界波長は小さくなり、より短い波長のゆらぎに対しても安定になります。 しかし \(\lambdacrit\) は、上層と下層の速度差が 0 でない限りは正の値を取るため、短い波長のゆらぎに対しては常に不安定であることが分かります。
- \(\rhop\gt\rhom\) のとき (レイリー・テイラー不安定のとき)、ゆらぎの波長によらず不安定
- \(\rhop \lt \rhom\) のとき (レイリー・テイラー不安定性に対して安定のとき)、
- 波長が \(\lambda\lt\lambdacrit\) のゆらぎは不安定 (ケルビン・ヘルムホルツ不安定性)
- 波長が \(\lambda\gt\lambdacrit\) のゆらぎは安定
- ただし \(\displaystyle{\lambdacrit=\frac{2\pi\rhop\rhom\left(\up-\um\right)^{2}}{g\left(\rhop+\rhom\right)\left(\rhom-\rhop\right)}}\)
- 速度差が大きいほど長波長のゆらぎも不安定になる
上層と下層に速度差が存在する場合は、たとえレイリー・テイラー不安定性に対して安定であっても、速度差に起因するケルビン・ヘルムホルツ不安定性によって不安定化されるということが分かります。 また、速度差が大きい場合はより長波長のゆらぎに対しても不安定になるということも分かります。
これは直感的には、風によって水面に立つ波の様子から理解することが出来ます。 水面の上を風が吹いているという状況は、下層に水、上層に空気があり、さらに上層と下層に速度差があるという状況に相当します。 風速が小さい場合は、ケルビン・ヘルムホルツ不安定性によって不安定化されるのは短い波長のゆらぎのみであり、水面には細かい波が立ちます。 しかし風速が大きい場合は臨界波長が大きくなるため、水面に波長の長いうねりが発達します。
ここまで見てきたケルビン・ヘルムホルツ不安定性およびレイリー・テイラー不安定性の条件や性質は、設定を簡単化してあるため必ずしも現実に即していない場合があります。
例えば境界面での表面張力による安定化作用を考慮していない点などです。
そこで、次には表面張力を考慮した場合の安定・不安定の条件やその性質について見ていきます。
ここまで見てきたレイリー・テイラー不安定性の条件では、上層の密度が下層の密度よりも大きい場合は、あらゆる波長のゆらぎに対して不安定になるということが分かりました。
また、ケルビン・ヘルムホルツ不安定性の条件では、2 層にわずかでも速度差があれば短波長のゆらぎは必ず不安定になるということが示されました。
しかしこれらの条件は簡単化されているため、必ずしも現実を反映していない場合があります。
先ほどの水面の上の風の例で言うと、風が極めて弱い状況であっても、速度差は 0 ではないため必ず短波長の波が立つことになりますが、実際は風速が小さすぎると波は立ちません。
これは、例えば粘性の効果や、境界面での表面張力の効果を無視している事が原因です。
ここでは、2 層の境界面での表面張力の効果を考慮して分散関係を導出し、2 層の境界面で起きる不安定性について見ていきます。
表面張力がある場合、運動方程式の \(z\) 成分である式 \eqref{eomz} は以下のように書き換えられます。
\begin{align*}
i\rho_{0}\left(-\omega+kv_{x0}\right)\delta w+\frac{d}{dz}\delta p +\delta\rho g=\sum_{\rm s}\left[T_{\rm s}\frac{\del^{2}}{\del x^{2}}\delta\zs\right]\delta\left(z-\zs\right)
\end{align*}
右辺に、外力の項として表面張力が加わっています。
ここで、\(T_{\rm s}\) は流体によって決まる係数、\(\delta\left(z-\zs\right)\) はディラックのデルタ関数です。
ゆらぎの微小量 \(\delta\zs\) は \(e^{i\left(kx-\omega t\right)}\) に比例することを考えると、この式は次のようになります。
\begin{align}
i\rho_{0}\left(-\omega+kv_{x0}\right)\delta w+\frac{d}{dz}\delta p +\delta\rho g=\sum_{\rm s}\left[k^{2}T_{\rm s}\delta\zs\right]\delta\left(z-\zs\right)
\label{eomzt}
\end{align}
ここで先程と同様に、両辺を境界面を挟んだ微小な範囲で積分すると、式 \eqref{eomzt} は
\begin{align*}
\delta\pp-\delta\pmi-g \left(\rhop-\rhom\right)\delta\zs=-k^{2}T\delta\zs
\end{align*}
となります (\(T\) は \(T_{\rm s}\) について足し合わせた値とします)。
これを整理すると以下のようになります。
\begin{align*}
\delta\pp-\delta\pmi=\left[g\left(\rhop-\rhom\right)-k^{2}T\right]\delta\zs
\end{align*}
さらに、式 \eqref{eomz} を \(z\gt0\) と \(z\lt0\) の範囲でそれぞれ考えたときと同様に、\eqref{eomzt} も \(z\gt0\) と \(z\lt0\) の範囲でそれぞれ考えます。
しかし右辺にはディラックのデルタ関数がありますが、境界面以外の場所では 0 となるため、結果として出て来る式は式 \eqref{eomzp} および \eqref{eomzm} と同じになります。
そのため、式 \eqref{disp} の分散関係において、\(g\left(\rhop-\rhom\right)\) を \(g\left[\left(\rhop-\rhom\right)-k^{2}T\right]\) に置き換えれば、表面張力の効果を考慮した場合の分散関係を得ることができることになります。
これまでと同様、根号の中が正の場合はゆらぎは指数関数的に成長して不安定、負であれば安定となります。
そのため、境界面での表面張力を考慮した不安定条件は
\begin{align}
\frac{k\rhop\rhom}{\left(\rhop+\rhom\right)^{2}}\left(\up-\um\right)^{2}+g\left(\frac{\rhop-\rhom}{\rhop+\rhom}-\frac{k^{2}T}{g\left(\rhop+\rhom\right)}\right)\gt0
\label{dispt2}
\end{align}
となります。
表面張力の効果は第 3 項に現れています。
表面張力の効果が大きい場合は第 3 項の影響が強くなるということに対応します。
式の形からは、第 3 項は左辺の値を小さくする方向に働く、つまり不安定条件を満たさない方向に働くことが分かります。
つまり、表面張力の項は系を安定化する方向に働いていることが分かります。
分散関係 \eqref{dispt} および、不安定条件の式 \eqref{dispt2} から、まずは表面張力の効果を考慮したレイリー・テイラー不安定性について考察します。
上層と下層の速度が 0 (\(\up=\um=0\)) という状況を考えます。
このとき、式 \eqref{dispt2} の不安定条件は、
\begin{align*}
g\left(\frac{\rhop-\rhom}{\rhop+\rhom}-\frac{k^{2}T}{g\left(\rhop+\rhom\right)}\right)\gt0
\end{align*}
となります。
これを整理すると、不安定条件は
\begin{align*}
\left(\rhop-\rhom\right)g-k^{2}T\gt0
\end{align*}
となります。
重い流体の上に軽い流体が乗っている状態、つまり \(\rhop\lt\rhom\) の場合は \(\rhop-\rhom\lt0\) であり、\(k\gt0\) かつ \(T\gt0\) なので常に安定条件 \(\left(\rhop-\rhom\right)g\lt k^{2}T\) を満たします。
つまり、\(\rhop\lt\rhom\) の場合は、波長によらずゆらぎは安定です。
次に、軽い流体の上に重い流体が乗っている状態、すなわち \(\rhop\gt\rhom\) の場合を考えます。
表面張力の効果を考えない場合、このときは波数 \(k\) (波長 \(\lambda\)) によらずゆらぎは不安定でした。
ここで、不安定条件を変形すると
\begin{align*}
k\lt\sqrt{\frac{\left(\rhop-\rhom\right)g}{T}}
\end{align*}
が得られます。
すなわち、ある波数より小さいゆらぎは不安定であるものの、ある波数以上のゆらぎは表面張力によって安定化されることが分かります。
この場合、ゆらぎが不安定化するのはゆらぎの波数 \(k\) が
\begin{align*}
0\gt k \gt \sqrt{\frac{\left(\rhop-\rhom\right)g}{T}}
\end{align*}
を満たす範囲のみとなります。
これを波長に直すと、ゆらぎが不安定になる波長の条件は
\begin{align*}
\lambda\gt 2\pi\sqrt{\frac{T}{\left(\rhop-\rhom\right)g}}
\end{align*}
となります。
つまり、軽い流体の上に重い流体が乗っているという状況であっても、一定の波長よりも短い波長を持つ揺らぎは、境界面での表面張力によって安定化されることが分かります。
式の形より、表面張力の係数 \(T\) が大きくなる (表面張力が強くなる) と、より長波長のゆらぎも表面張力の効果によって安定になることが分かります。
この点が、表面張力を考慮しなかった場合の、\(\rhop\gt\rhom\) の時はゆらぎの波長 (波数) に関わらず不安定という条件と異なる部分です。
ただし、表面張力の効果を考慮しても大きい波長のゆらぎに対しては依然として不安定です。
そのため、境界面に与えるゆらぎが様々な波長を含んでいる場合、いずれ長波長のゆらぎが成長して不安定となります。
続いて、レイリー・テイラー不安定性に対して安定である \(\rhop\lt\rhom\) の状態を考えます。
表面張力の影響を考慮しない場合は、レイリー・テイラー不安定性に対して安定である場合であっても、上層と下層に速度差が存在する場合は短波長のゆらぎに対しては必ずケルビン・ヘルムホルツ不安定性が発達するのでした。
ここでは、表面張力が働いた結果として系がケルビン・ヘルムホルツ不安定性に対して安定化される状況を考えます。
分散関係 \eqref{dispt} より、不安定条件は式 \eqref{dispt2} で表されました。
従って,安定条件は
\begin{align}
\frac{k\rhop\rhom}{\left(\rhop+\rhom\right)^{2}}\left(\up-\um\right)^{2}+g\left(\frac{\rhop-\rhom}{\rhop+\rhom}-\frac{k^{2}T}{g\left(\rhop+\rhom\right)}\right)\lt0
\label{dispt3}
\end{align}
で表されます。
この安定条件を波数 \(k\) について整理すると、
\begin{align*}
\frac{T}{\rhop+\rhom}k^{2}-\frac{\rhop\rhom}{\left(\rhop+\rhom\right)^{2}}\left(\up-\um\right)^{2}k-\frac{\rhop-\rhom}{\rhop+\rhom}g\gt0
\end{align*}
となります。
これは \(k\) についての 2 次不等式になっています。
ここで、波数 \(k\) によらずこの不等式が満たされるための条件を考えます。
そのためには、不等式の左辺の最小値が正となればよいという事になります。
\begin{align*}
\left(左辺の最小値\right)\gt0
\end{align*}
という式を整理すると、
\begin{align*}
\left(\up-\um\right)^{4}\lt-4\frac{\left(\rhop-\rhom\right)^{2}}{\rhop^{2}\rhom^{2}}Tg\left(\rhop-\rhom\right)
\end{align*}
となり、
\begin{align*}
\left(\up-\um\right)^{4}\lt\frac{4\left(\rhop-\rhom\right)^{2}}{\rhop^{2}\rhom^{2}}Tg\left(\rhom-\rhop\right)
\end{align*}
が得られます。
いまは \(\rhop\lt\rhom\) の状態を考えているため、\(\rhom-\rhop\gt0\) です。
従って、境界面でのゆらぎの波数 \(k\) によらず安定であるための条件は、
\begin{align}
\left(\up-\um\right)^{2}\lt\frac{2\left(\rhop+\rhom\right)}{\rhop\rhom}\sqrt{Tg\left(\rhom-\rhop\right)}
\label{dispt4}
\end{align}
となります。
あるいは
\begin{align*}
\abs{\up-\um}\lt\sqrt{\frac{2\left(\rhop+\rhom\right)}{\rhop\rhom}}\sqrt[4]{Tg\left(\rhom-\rhop\right)}
\end{align*}
と書くことも出来ます。
つまり、2 層の速度差の 2 乗が式 \eqref{dispt4} の右辺よりも小さい場合は、あらゆる波数 \(k\) で (つまりあらゆる波長で) 安定であることが分かります。
レイリー・テイラー不安定性に対して安定な場合 (\(\rhop\lt\rhom\)) で速度差があるとき、表面張力を考えない場合は短波長のゆらぎが必ず不安定になりました。
しかし式 \eqref{dispt4} より、表面張力の効果を考えると 2 層の速度差が小さい場合は表面張力による安定化が効き、あらゆる波長のゆらぎに対して安定になることが分かります。
そのためこの場合はケルビン・ヘルムホルツ不安定性は発生しません。
逆に、2 層の速度差が一定値より大きい場合は、波数によっては不安定なモードが存在するため、系が不安定になる波長が存在することになります。
応用版として、重力の影響が無い場合を考えます。
これは例えば、上下に 2 層の流体が重なって存在しているのではなく、水平方向に流れる 2 つの流体に速度差が存在する、というような状況に対応しています。
式 \eqref{disp} で \(g=0\) とした場合が、重力項が存在しない場合の分散関係になります。
その式は以下のように書けます。
\begin{align*}
\omega=k\frac{\rhop\up+\rhom\um}{\rhop+\rhom}\pm i\sqrt{\frac{k^{2}\rhop\rhom}{\left(\rhop+\rhom\right)^{2}}\left(\up-\um\right)^{2}}
\end{align*}
ゆらぎが指数関数的に成長して不安定になるための条件は、これまでと同様に、根号の中が正の値になることです。
従って、この場合の不安定条件は
\begin{align*}
\frac{k^{2}\rhop\rhom}{\left(\rhop+\rhom\right)^{2}}\left(\up-\um\right)^{2}\gt0
\end{align*}
となります。
2 層の速度差が存在しない場合は左辺は 0 になるため安定となりますが,速度差が存在する場合は左辺は波数 \(k\) に関わらず正の値になることが分かります。
そのため、流体に速度差が存在する場合は、ゆらぎの波数 (波長) に関わらず不安定です。
これは、水平方向に隣り合った 2 つの流体に速度差が存在する場合は、かならず境界面のゆらぎは不安定になるということを意味します。
一方、境界面での表面張力を考慮した場合の分散関係は式 \eqref{dispt} で与えられます。
ここで \(g=0\) とすると、分散関係は
\begin{align*}
\omega=k\frac{\rhop\up+\rhom\um}{\rhop+\rhom}\pm i\sqrt{\frac{k^{2}\rhop\rhom}{\left(\rhop+\rhom\right)^{2}}\left(\up-\um\right)^{2}-\frac{k^{3}T}{\left(\rhop+\rhom\right)}}
\end{align*}
となります。
従って不安定条件は
\begin{align*}
\frac{k^{2}\rhop\rhom}{\left(\rhop+\rhom\right)^{2}}\left(\up-\um\right)^{2}-\frac{k^{3}T}{\left(\rhop+\rhom\right)}\gt0
\end{align*}
となります。
\(k\gt0\) より、上記の不安定条件は
\begin{align*}
Tk-\frac{\rhop\rhom}{\rhop+\rhom}\left(\up-\um\right)^{2}\lt0
\end{align*}
となります。
そのため、
\begin{align*}
k\lt\frac{\rhop\rhom}{\rhop+\rhom}\frac{\left(\up-\um\right)^{2}}{T}
\end{align*}
を満たす波数の時にゆらぎは不安定になることが分かります。
波数を波長に書き直すと、不安定条件は
\begin{align*}
\lambda\gt 2\pi\frac{\rhop+\rhom}{\rhop\rhom}\frac{T}{\left(\up-\um\right)^{2}}
\end{align*}
となります。
従って表面張力を考慮した場合は、先ほどまでの考察と同様に、短波長のゆらぎは表面張力によって安定化されることが分かります。
表面張力が大きくなれば、すなわち \(T\) が大きくなれば、より長波長のゆらぎも安定化されます。
また、速度差が大きくなると安定と不安定の境目となる波長は小さくなり、より短波長のゆらぎも不安定になるということが分かります。
レイリー・テイラー不安定性は、ここまで見てきた通り軽い流体の上に重い流体が乗っている状態で、2 層の境界面で発達する不安定性です。
そのようなきれいな初期条件を実際に作るのはなかなか難しいですが、軽い液体の上に静かに重い液体を注ぐと、重い液体が軽い液体の方へ指を伸ばすように侵入し、軽い液体は逆に上昇して混ざり合っていく様子が観察できます。
数値計算でもその様子を確認することが出来ます。
2 層の境界面でレイリー・テイラー不安定性が発達して混ざり合う様子のスナップショットが、例えば以下のサイトで紹介されています。
また、ここでは \(z\) 軸の下向きに重力がかかっていて、上層に重い流体、下層に軽い流体がそれぞれ静止して存在するという状況を主に考えていましたが、流体が加速度運動をしている状況でもレイリー・テイラー不安定性が発生します。
例えば星間物質中を衝撃波が伝わって加速度運動しているとき、希薄なガスが高密度のガスを押しているという状況になっている時は、ガスの境界面でレイリー・テイラー不安定性が発達し、ガスの混合が起きます。
このようなレイリー・テイラー不安定性による物質の混合は、超新星の内部での衝撃波や、超新星残骸などでも発生し、物質の混合という観点で非常に重要な現象です。
ケルビン・ヘルムホルツ不安定性は、異なる密度を持つ流体が速度差を持って接している場合に発生します。
風が吹いた時の水面に立つ波の特徴はケルビン・ヘルムホルツ不安定性から理解が出来ましたが、さらに不安定が発達した例としては大気中でのケルビン・ヘルムホルツ不安定性があります。
大気はその状況によって様々な状態を取ります。
例えば大気の下層はほとんど流れがないものの、上空では風が吹いている、という状況は容易に実現されます。
そのような場合、速度差があることによって 2 層の境界面でケルビン・ヘルムホルツ不安定性が発達することがあります。
大気中でケルビン・ヘルムホルツ不安定性が発生している際に、層の片方に雲が存在するなどして、不安定による渦が可視化される場合があります。
これは波状雲の一種であり、条件が整うときれいに揃った渦状の雲の列として見ることが出来ます。
また、水平方向に隣り合った 2 流体に速度差がある場合のケルビン・ヘルムホルツ不安定性は、例えば土星の大気中などガス惑星の大気でも見られます。
表面張力が働く場合
表面張力を考慮した線形不安定性解析
表面張力が働く場合のレイリー・テイラー不安定性
表面張力が働く場合のケルビン・ヘルムホルツ不安定性
重力項が無い場合
不安定性の実例
レイリー・テイラー不安定性の実例
Parallel AMR Code for Compressible MHD or HD Equations
ケルビン・ヘルムホルツ不安定性の実例
例:ケルビン・ヘルムホルツ不安定性 - Wikipedia
参考文献
坂下志郎・池内了「宇宙流体力学」(培風館)
観山正見・野本憲一・二間瀬敏史編「天体物理学の基礎I」(日本評論社)
福江純・和田桂一・梅村雅之編「宇宙流体力学の基礎」(日本評論社)
2017年07月13日