はじめに
大学に入るとベクトル演算をする機会が増えるかと思います。
ベクトルの計算は往々にして煩雑ですが、特に球座標などの曲がった座標系の場合のベクトル演算はさらに煩雑なものになります。
ここでは、3次元球座標における、ベクトルの勾配(gradient)、発散(divergence)、回転(rotation)、ラプラシアンの表式と簡単な導出方法を、備忘録を兼ねてまとめておきたいと思います。
まず先に式を書くと以下の通りになります。
3次元球座標系におけるスカラー関数の勾配は
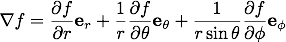
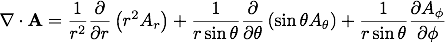
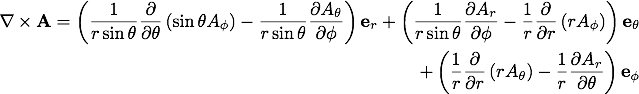
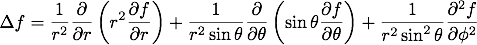
ここで、
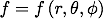 はスカラー関数、
はスカラー関数、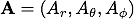 はベクトル関数です。
はベクトル関数です。
- 導出のための下準備
- 座標変換
- 単位ベクトルの変換
- 偏微分演算子の変換
- 単位ベクトルの微分
- 単位ベクトルの外積
- 球座標での勾配(gradient)
- 球座標での発散(divergence)
- 球座標での回転(rotation)
- 球座標でのラプラシアン
- PDFファイル
導出のための下準備
座標変換
直交座標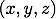 から球座標
から球座標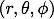 への座標変換を行います。
両者の関係は、
への座標変換を行います。
両者の関係は、
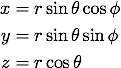
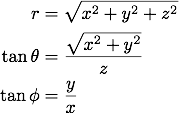
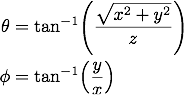
単位ベクトルの変換
直交座標における単位ベクトル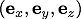 と、球座標における単位ベクトル
と、球座標における単位ベクトル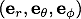 の関係を導出しておきます。
球座標での単位ベクトルはそれぞれ、
の関係を導出しておきます。
球座標での単位ベクトルはそれぞれ、
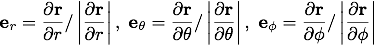
この式に、
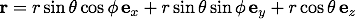 を代入して計算することによって球座標での単位ベクトル
を代入して計算することによって球座標での単位ベクトル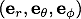 と直交座標での単位ベクトル
と直交座標での単位ベクトル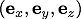 の関係を求めることが出来ます。
それぞれ計算すると、
の関係を求めることが出来ます。
それぞれ計算すると、
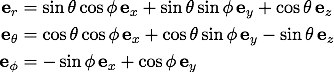
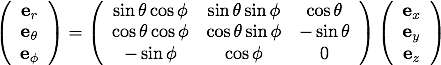
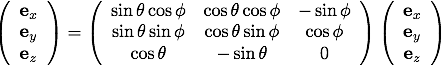
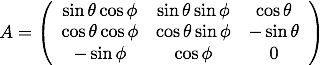
偏微分演算子の変換
続いて、直交座標での偏微分演算子と球座標での偏微分演算子の対応関係を求めます。 偏微分演算子には以下の対応関係があります。
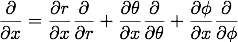
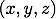 と
と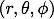 の関係式から係数部分は計算出来て、
の関係式から係数部分は計算出来て、
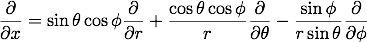
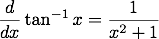
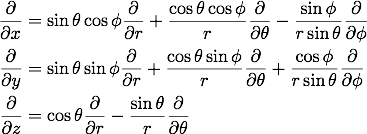
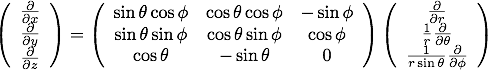
単位ベクトルの微分
単位ベクトルを微分した際の関係式を導出しておきます。
この先の導出において、単位ベクトルの微分は非常に重要です。
直交座標では、単位ベクトル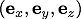 を
を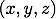 で偏微分しても0になりますが、球座標ではそうなりません。
「単位ベクトルの変換」の部分で、球座標での単位ベクトルを
で偏微分しても0になりますが、球座標ではそうなりません。
「単位ベクトルの変換」の部分で、球座標での単位ベクトルを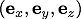 を使って表したので、その式を
を使って表したので、その式を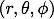 で偏微分します。
偏微分を行ったあとに
で偏微分します。
偏微分を行ったあとに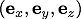 を
を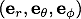 で書き直してやると、以下の関係式を得ます。
で書き直してやると、以下の関係式を得ます。
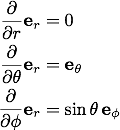
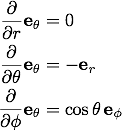
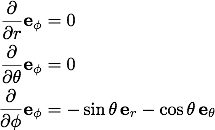
単位ベクトルの外積
ベクトル関数の回転を求める際には単位ベクトル同士の外積も必要なので先に示しておきます。 球座標の単位ベクトルの外積は
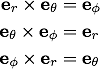
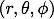 で右手系になっています。
外積の順序が逆であれば右辺はマイナスが付きます。
で右手系になっています。
外積の順序が逆であれば右辺はマイナスが付きます。
球座標での勾配(gradient)
まず、任意のスカラー関数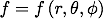 の勾配(gradient)を導出します。
直交座標での勾配は、直交座標での偏微分演算子と単位ベクトルを用いて
の勾配(gradient)を導出します。
直交座標での勾配は、直交座標での偏微分演算子と単位ベクトルを用いて
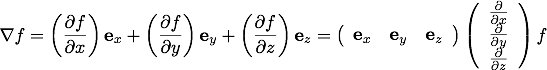
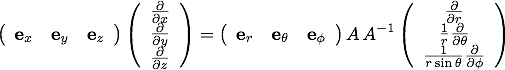
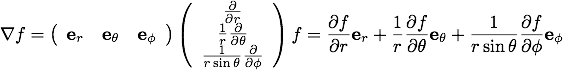
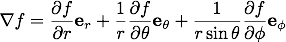
また、この式からスカラー関数を省いて微分ベクトル演算子の形で書くと、
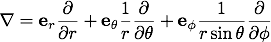
球座標での発散(divergence)
次に、任意のベクトル関数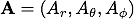 の発散(divergence)を導出します。
ベクトル関数は次のように成分表記することが出来ます。
の発散(divergence)を導出します。
ベクトル関数は次のように成分表記することが出来ます。
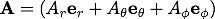
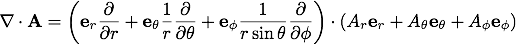
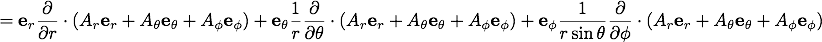
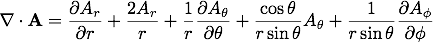
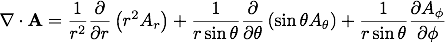
球座標での回転(rotation)
続いて、任意のベクトル関数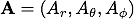 の回転(rotation)を導出します。
先ほど同様に考えると、
の回転(rotation)を導出します。
先ほど同様に考えると、
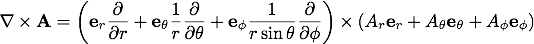
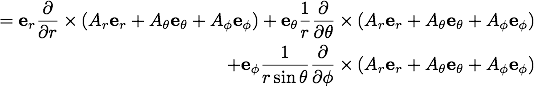
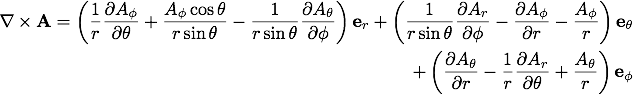
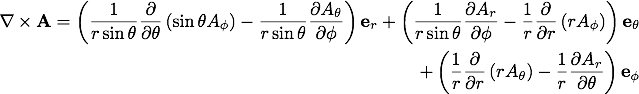
球座標でのラプラシアン
最後に、球座標でのラプラシアンの表式を導出します。
任意のスカラー関数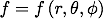 にラプラシアンを作用させたものは、
にラプラシアンを作用させたものは、
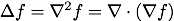
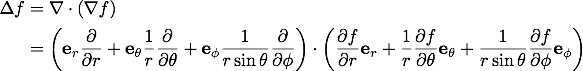
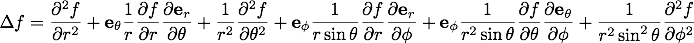
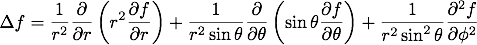
また、演算子の部分だけ取り出すと、
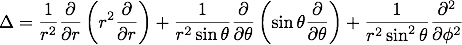
以上の計算はPDF文書にまとめました。
ここに載せたものより少しだけ詳細な計算も書いてあります。
PDFファイル
2017年04月24日 更新