静水圧平衡

　まずは静的な大気を考え、そこにはたらく力の釣り合いから静水圧平衡の式を求めます。 ある微小領域の大気にはたらく力が釣り合っていれば、大気は動かずに静止しているということになります。

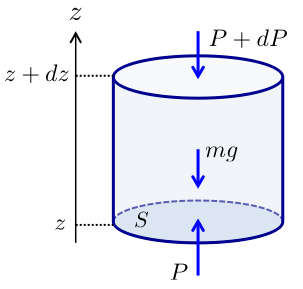
　上図のような円筒状の領域と、そこにかかる力を考えます。 鉛直上向きを \(z\) 軸の正の方向に取ります。 円筒下部での気圧を \(P\) とすると、円筒の下面に加わる力の大きさは圧力に面積をかけた \(PS\) となり、向きは鉛直上向きです。 また、円筒上部での気圧を \(P+dP\)とすると、同様に円筒の上面に加わる力の大きさは \(\left(P+dP\right)S\)、向きは鉛直下向きです。 ここでは特に指定はしていませんが、大気を考えているので上空に行くほど気圧は小さくなる場合は \(dP\) は負の値となります。 次に、円筒にはたらく重力は円筒全体の質量を \(m\) とすると \(mg\) となりますが、円筒内の気体の密度を \(\rho\) とすると \(mg=\rho Sdzg\) と書くことができます。 向きは鉛直下向きです。 以上より、円筒にはたらく力の釣り合いの式は、 \begin{align*} PS=\left(P+dP\right)S+\rho S g dz \end{align*} と書くことができます。 これを整理すると次の式になります。 \begin{align*} \frac{dP}{dz}=-\rho g \end{align*} これが、円筒にはたらく力の釣り合いから求めた静水圧平衡の式です。

　この式の両辺を密度で割ると \begin{align*} \frac{1}{\rho}\frac{dP}{dz}=-g \end{align*} となります。 右辺は重力加速度、あるいは単位質量あたりにはたらく重力を意味します。 左辺は、圧力の差があることによってはたらく加速度、あるいは圧力の差があることによって単位質量あたりにはたらく力を意味します。 このような、圧力に差があることによってはたらく力の事を、圧力勾配力 (pressure gradient force) と呼びます。 大気中で、重力と圧力勾配力が釣り合っている状態のことを静水圧平衡 (hydrostatic equilibrium) と呼びます。

静水圧平衡の一般形

　静水圧平衡の式は圧力 \(P\) についての微分方程式になっていて、これを \(z\) について積分すれば鉛直方向の圧力分布が計算出来ることになります。 しかし、圧力、密度と温度の関係が不明であるためこのままでは微分方程式を解くことができません。 それぞれを結びつける式としては、気体の状態方程式があります。

　理想気体の状態方程式として恐らく最も知られているのは、高校物理の範囲でも取り扱う次の形だと思われます。 \begin{align*} PV=nRT \end{align*} \(P\) [Pa] は圧力、\(V\) [m³] は体積、\(n\) [mol] は含まれる気体の物質量、\(T\) [K] は気体の温度です。 また、\(R\) は気体定数 (gas constant) で、\(R\) = 8.3144621 J K^-1 mol^-1です。

　気体定数 \(R\) には、次のような関係があります。 \begin{align*} R=\NA\kB \end{align*} ここで \(\NA\) はアボガドロ定数 (Avogadro constant) で \(\NA\) = 6.02214129 × 10²³ mol^-1、 \(\kB\) はボルツマン定数 (Boltzmann constant) で \(\kB\) = 1.3806488 × 10^-23 J K^-1 です。 これを用いて気体定数を消去すると、理想気体の状態方程式は \begin{align*} PV=n\NA\kB T \end{align*} となります。 ここで、系に含まれる物質量 \(n\) とアボガドロ定数 \(\NA\) の積は、系に含まれる全粒子数に他なりません。 従って、全粒子数を \(N\) とすると、\(N=n\NA\) と書くことができます。 よって、状態方程式は以下のように書き表すことができます。 \begin{align*} PV=N\kB T \end{align*} この表式は、しばしば統計力学で使われます。

　もう一度一般的な表式に戻ります。 \begin{align*} PV=nRT \end{align*}

　物質量 \(n\) は、気体の全質量をその気体のモル質量 (molar mass) で割る事で求めることができます。 モル質量とは、物質 1 mol あたりの質量に相当します。 例えば水分子のモル質量はおよそ 18.0 × 10^-3 kg mol^-1 あるいは 18.0 g mol^-1であり、水 1 mol の質量は 18.0 g です。 気体の全質量を \(M_{\rm total}\) [kg]、その気体のモル質量を \(M\) [kg mol^-1] とすると、物質量 \(n\) [mol] は \(n=M_{\rm total}/M\) で与えられます。 気体が混合物である場合は、平均したモル質量を計算に用います。 モル質量を用いて状態方程式を書き直すと以下のようになります。 \begin{align*} PV=\frac{M_{\rm total}}{M}RT \end{align*} 一方、気体の質量を体積で割ったものは密度 (質量密度) になります。 すなわち、密度 \(\rho\) [kg m^-3]は \(\rho=M_{\rm total}/V\) となります。 これを用いると、状態方程式はさらに次のように書き直すことができます。 \begin{align*} P=\frac{\rho RT}{M} \end{align*} これが、モル質量を用いた形式の理想気体の状態方程式です。

比気体定数

　上の状態方程式に対して、気体定数をモル質量で割った値を比気体定数 (specific gas constant) と呼ぶ事があります。 比気体定数は次のように表されます。 \begin{align*} R_{\rm spe}=\frac{R}{M} \end{align*} 比気体定数を用いると、状態方程式は \begin{align*} P=\rho R_{\rm spe}T \end{align*} という形で表されます。

　気体定数は気体の種類や混合比に関係なく一定の値を持つ定数ですが、定義より明らかなように、比気体定数は気体の種類や混合比によって異なる値を持つ量です。 気体定数 \(R\) は [J K^-1 mol^-1] の次元を持ちますが、気体定数をモル質量で割った値である比気体定数\(R_{\rm spe}\) の次元は[J kg^-1 K^-1] です。

　取り扱う気体の種類が変わらない場合は、気体定数よりも比気体定数を用いた方が便利な場合があります。 そのためか、特に工学の分野においては比気体定数のことを指して気体定数と呼び、単に \(R\) のみで表すことがあります。 このような場合は、(本来の) 気体定数を \(\bar{R}\) と表記して区別します。 また、特に区別をする場合は普遍気体定数 (universal gas constant) と表現します。

　次に平均分子量を用いた表式を導出します。 先ほど導出した、統計力学でよく使われる表式は以下の通りです。 \begin{align*} PV=N\kB T \end{align*} ここで、平均分子量 (mean molecular mass) \(\mu\) を導入します。 考えているガスの平均的な分子量を表します。 また、統一原子質量単位 (unified atomic mass unit) \(\munit\) を導入します。 統一原子質量単位は質量を表す単位であり、束縛されず静止した状態で基底状態にある、中性の ¹²C 原子の質量の 12 分の 1 と定義されています。 単位 [u] を用いて \(\munit=1\,{\rm u}=1.660538921\times10^{-27}\,{\rm kg}\) と表します。 ¹²C 原子は、陽子 6 個・中性子 6 個からなる原子核と、電子 6 個からなる原子なので、それを 12 で割った統一原子質量単位は、核子 1 個の平均的な質量に近い値になります。

　平均分子量 \(\mu\) と \(\munit\) の積 \(\mu\munit\) は、系に含まれる粒子の平均質量を表します。 よって、\(\mu\munit\) に全粒子数 \(N\) をかけた値は、系の気体の全質量となります。 \begin{align*} M_{\rm total}=\mu\munit N \end{align*} この関係を用いて状態方程式を書き直すと、 \begin{align*} P=\frac{N\kB T}{V}=\frac{M_{\rm total}}{V}\frac{\kB T}{\mu\munit}=\frac{\rho\kB T}{\mu\munit} \end{align*} となります。 よって、平均分子量を用いた場合の理想気体の状態方程式は以下のように書き表されます。 \begin{align*} P=\frac{\rho\kB T}{\mu\munit} \end{align*}

水素原子質量を用いた場合

　上記の状態方程式は、統一原子質量単位 \(\munit\) を用いず、水素原子の質量 \(\mH\) を用いて以下のように書かれている場合もあります。 \begin{align*} P=\frac{\rho\kB T}{\mu\mH} \end{align*} 　\(\munit\) の値は核子 1 個の値と近い値になりますが、厳密には異なる値になります。 例としては、\(\munit=1\,{\rm u}\) であるのに対して、陽子質量 \(m_{\rm p}\)、中性子質量 \(m_{\rm n}\)、中性水素原子 \(\mH\) の質量はそれぞれ次のようになります。 \begin{align*} m_{\rm p}=1.00727646681\,{\rm u}\\ m_{\rm n}=1.0086649160\,{\rm u}\\ \mH=1.00782503297\,{\rm u} \end{align*} 単独の陽子 2 個と中性子 2 個の合計質量が、それらが結合して出来たヘリウム原子核の質量と等しくならないように、結合エネルギーの分だけ質量に差が出ます。 また、陽子と中性子の質量はそもそも同じではありません。 そのため、¹²C 原子の質量を 12 で割ったものと、陽子質量や水素原子の質量などは近い値になるものの、一致はしません。

　以下に、状態方程式の様々なパターンをまとめます。 物理量の単位は便宜上 SI 単位系 (あるいは MKSA 単位系) で書いてあります。

大気のスケールハイト

　まずは、静水圧平衡の式を解きます。 解くべき式と、物理量を関係付ける状態方程式は次の通りです。 \begin{align*} \frac{dP}{dz}=-\rho g \end{align*} \begin{align*} P=\frac{\rho\kB T}{\mu\munit} \end{align*}

　理想気体の状態方程式の両辺を \(z\) で微分します。 圧力 \(P\)、密度 \(\rho\)、温度 \(T\) がそれぞれ高さ \(z\) の関数だとすると、微分した結果は \begin{align*} \frac{dP}{dz}=\frac{\kB T}{\mu\munit}\frac{d\rho}{dz}+\frac{\rho\kB}{\mu\munit}\frac{dT}{dz} \end{align*} となります。 ここで、大気は等温 (isothermal) であるという仮定を置きます。 温度が高度によって変化しない、すなわち温度の \(z\) 微分がゼロという事なので、状態方程式の \(z\) 微分は \begin{align*} \frac{dP}{dz}=\frac{\kB T}{\mu\munit}\frac{d\rho}{dz} \end{align*} となります。 もちろん実際の大気は高度依存性があるため厳密には正しくありませんが、一般に大気のスケールハイトを計算する際には等温大気の仮定をすることが多いです。 温度の高度依存性がある一般的な場合については後で簡単に触れます。

　この式を用いて、静水圧平衡の式から \(P\) を消去すると、 \begin{align*} \frac{d\rho}{dz}=-\frac{\mu\munit g}{\kB T}\rho \end{align*} となります。 ここで右辺の係数部分を \(\displaystyle{\frac{\mu\munit g}{\kB T}=\frac{1}{H_{0}}}\) と置くと、微分方程式は \begin{align*} \frac{d\rho}{dz}=-\frac{1}{H_{0}}\rho \end{align*} となります。 変数分離形にすると \begin{align*} \frac{d\rho}{\rho}=-\frac{dz}{H_{0}} \end{align*} となり、両辺を積分すると \begin{align*} \ln\rho=-\frac{z}{H_{0}}+C^{\prime} \end{align*} になります。 \(C^{\prime}\) は積分定数です。 この式は \begin{align*} \rho\!\left(z\right)=C\exp\left(-\frac{z}{H_{0}}\right) \end{align*} と書き直すことができます。 \(C\) は同じく積分定数です。 境界条件を、高度がゼロ、すなわち \(z=0\) で密度が \(\rho_{0}\) になるとすると、密度分布の式は以下のようになります。 \begin{align*} \rho=\rho_{0}\exp\left(-\frac{z}{H_{0}}\right) \end{align*} \begin{align*} H_{0}=\frac{\kB T}{\mu\munit g} \end{align*} と書くことができます。

　この式を見ると、密度は指数関数的に減少し、高度が \(z=H_{0}\) となる場所で、密度が地上の密度の \(1/e\) 倍になっていることが分かります。 このような、元の量の \(1/e\) になるまでの距離や高度 \(H_{0}\) の事を、スケールハイトと呼び、指数関数的に減少する際の系の典型的な長さにあたります。

　状態方程式の表現に様々な種類があるのと同様に、スケールハイトも様々な書き方が出来ます。 例えば、気体定数と平均モル質量を用いた場合のスケールハイトの表式は \begin{align*} H_{0}=\frac{RT}{Mg} \end{align*} となります。 使われている文字は異なりますが、値は同じです。

圧力分布の導出

　上では圧力を消去して密度について解きましたが、密度を消去して圧力分布を導出する事も出来ます。 状態方程式を微分せず、そのまま静水圧平衡の式に代入して密度を消去すると、 \begin{align*} \frac{dP}{dz}=-\frac{\mu\munit g}{\kB T}P=-\frac{1}{H_{0}}P \end{align*} となります。 これも密度の時と同じように解いてやれば、次のような圧力分布の式が得られます。 \begin{align*} P\!\left(z\right)=P_{0}\exp\left(-\frac{z}{H_{0}}\right) \end{align*} \(P_{0}\) は高度ゼロ、すなわち地表での圧力 (気圧) です。

　式を見ると分かるように、等温大気の場合は密度と圧力の高度依存性は同じ形で表され、密度のスケールハイトと圧力のスケールハイトは同じになります。

スケールハイトから分かる事

　大気のスケールハイトは、大気を扱う時のあちこちに顔を出します。 ここではその一部を紹介します。

大気の柱密度

　得られた密度を、\(z\) 方向に積分します。 積分範囲は、0 (地表面) から無限遠までです。 \begin{align*} \int_{0}^{\infty}=\rho\!\left(z\right)dz=\rho_{0}\int_{0}^{\infty}\exp\left(-\frac{z}{H_{0}}\right)dz=\rho_{0}H_{0} \end{align*}

　密度を \(z\) で 0 から無限遠まで積分すると、地表面での密度にスケールハイトをかけた形になることが分かります。 これは、質量を面積で割った次元を持っています。 つまり、密度を [kg m^-3]、スケールハイトが [m] だとすると、これは [kg m^-2] という次元になります。 これは単位面積あたりの大気の質量を意味します。 これを大気の柱密度 (column density)と呼びます。 ある単位面積の上にある無限遠まで続く柱の中にある大気の質量を表しているため、このような名前で呼ばれます。

　単位面積あたりの大気質量が、地表面での密度とスケールハイトの積で書けるということは、全ての大気を表面での密度に圧縮した場合、その厚みはスケールハイトと等しくなるという事になります。

大気の重心の位置

　地表から測った時の大気の重心の位置 \(h_{\rm g}\) は、次の式で計算出来ます。 \begin{align*} h_{\rm g}=\frac{\int_{0}^{\infty}z\rho\!\left(z\right)dz}{\int_{0}^{\infty}\rho\!\left(z\right)dz} \end{align*}

　分子の部分を計算すると以下のようになります。 \begin{align*} \int_{0}^{\infty}z\rho\!\left(z\right)dz&=\rho_{0}\int_{0}^{\infty}z\exp\left(-\frac{z}{H_{0}}\right)dz\\ &=\rho_{0}\left(-\left[H_{0}z\exp\left(-\frac{z}{H_{0}}\right)\right]_{0}^{\infty}+\int_{0}^{\infty}H_{0}\exp\left(-\frac{z}{H_{0}}\right)dz\right)\\ &=\rho_{0}\left(H_{0}\left[-H_{0}\exp\left(-\frac{z}{H_{0}}\right)\right]_{0}^{\infty}\right)\\ &=\rho_{0}H_{0}^{2} \end{align*}

　よって、大気の重心の位置は \begin{align*} h_{\rm g}=\frac{\int_{0}^{\infty}z\rho\!\left(z\right)dz}{\int_{0}^{\infty}\rho\!\left(z\right)dz}=\frac{\rho_{0}H_{0}^{2}}{\rho_{0}H_{0}}=H_{0} \end{align*} となり、大気の重心の位置は地表からスケールハイト分だけ進んだ場所であることが分かります。

大気の全質量

　スケールハイトなどを用いて、大気の全質量を概算する事も出来ます。 大気の柱密度の部分では、単位面積あたりの大気の質量を計算しました。 そのため、柱密度に地球の表面積をかければ、大気の全ての質量になることが分かります。

　惑星の半径を \(R_{\rm p}\) とすると、大気の全質量は \(\rho_{0}H_{0}\cdot4\pi R_{\rm p}^{2}\) で計算出来ることになります。 具体的な数値は後ほど紹介します。

スケールハイトを決める物理量

　スケールハイトの表式は、 \begin{align*} H_{0}=\frac{RT}{Mg} \end{align*} で与えられました。 ここで、\(R\) は気体定数、\(T\) は大気の温度、\(M\) は平均モル質量、\(g\) は重力加速度です。

　\(R\) は定数であるため、スケールハイトに影響を及ぼすのは残りの 3 つの物理量になります。
　分子に温度 \(T\) が入っているため、これは大気の温度が高いほどスケールハイトは大きくなるということを意味します。 直感的には、温度が高いほど気体は膨張して大気層はより広がり、逆に温度が低いと収縮して大気層も薄くなるということに対応しています。

　分母に平均モル質量 \(M\) がありますが、平均モル質量はおおまかに言えば大気の重さを表しています。 \(M\) が大きいほど、つまりその天体の大気が重いほどスケールハイトは小さくなり、大気層は薄くなります。 二酸化炭素主体の重い大気よりも、水素主体の軽い大気の方が大気層が大きく広がりそうですが、この感覚に対応しています。

　スケールハイトの表式 \(\displaystyle{H_{0}=\frac{RT}{Mg}}\) を用いて、様々な天体のスケールハイトを計算してみます。

地球

　地球の平均気温を 288 K、重力加速度を 9.80665 m s^-2 とします。 まずは平均モル質量を計算する必要があります。 そこで、地球大気の組成から計算します。 地球の大気の主要な組成は、

• 窒素 78.08%
• 酸素 20.95%
• アルゴン 0.934%
• 二酸化炭素 0.04%

　これらの値と、気体定数 \(R\) = 8.3144621 J K^-1 mol^-1 を用いてスケールハイトを計算すると、8432.24867...m となるため、地球大気のスケールハイトは ~ 8.4 km となります。

　スケールハイトが 8.4 km ということは、標高 8.4 km の地点で気圧が地上の気圧の \(1/e\) 倍 ( ~ 0.358 倍) になるということです。 参考として、エベレストの標高は 8848 m で、その頂上付近での気圧は地上の 3 分の 1 程度になっているため、おおむね一致していることが分かります。

　密度や圧力は \begin{align*} \rho\!\left(z\right)=\rho_{0}\exp\left(-\frac{z}{H_{0}}\right) \end{align*} \begin{align*} P\!\left(z\right)=P_{0}\exp\left(-\frac{z}{H_{0}}\right) \end{align*} で表されるため、ここから標高と気圧の関係を計算することができます。

　例えば富士山の山頂 (標高 3776 m) での気圧を計算すると、地上での大気圧 \(P_{0}\) を 1013.25 hPa として圧力の関係式に代入すると、647.50 hPa、およそ 650 hPa となります。 これは実際の富士山山頂での平均的な気圧におおむね近い値になります。 また、エベレストの山頂での値を計算するとおよそ 355 hPaとなります。

　また、静水圧平衡の式から導出した圧力に関する微分方程式は、以下のように書けました。 \begin{align*} \frac{dP}{dz}=-\frac{\mu\munit g}{\kB T}P=-\frac{1}{H_{0}}P \end{align*} この式の右辺のPに地上での大気圧を代入すると、\(\left(dP/dz\right)\) = -0.12 hPa m^-1 となります。 つまり、地上付近では標高が 1 m 上昇するごとに 0.12 hPa 気圧が低下するということになります。 実際には標高 1 m につき気圧はおおよそ 0.1 hPa 低下すると言われており、おおむね近い値が得られました。

火星

　次に火星大気のスケールハイトを計算します。 火星の平均気温を 210 K、重力加速度を 3.71 m s^-2 とします。 火星の大気組成は、

• 二酸化炭素 95.32%
• 窒素 2.7%
• アルゴン 1.6%
• 酸素 0.13%

　スケールハイトを計算すると、11366.0458...m となるため、火星大気のスケールハイトは ~ 11.4 km となります。

　二酸化炭素主体の火星大気は、窒素主体の地球大気よりも平均モル質量は大きくなります。 これはスケールハイトを小さくする方向にはたらきますが、火星の気温が低い事に加え、重力加速度が地球の 38% 程度しかないため、火星大気のスケールハイトは地球のものよりも大きくなります。

金星

　金星の平均気温を 737 K、重力加速度は 8.87 m s^-2 とします。 金星の大気組成は、

• 二酸化炭素 96.5%
• 窒素 3.5%
• 二酸化硫黄 0.015%

　スケールハイトを計算すると 15899.8213...m であり、金星大気のスケールハイトは ~ 15.9 km となります。

　金星大気の平均モル質量は火星と同様に地球より大きくなります。 金星は質量・半径ともに地球よりやや小さい程度であるため、表面での重力は地球とは大差ありません。 しかし、表面温度が 737 K と圧倒的に異なるため、スケールハイトも地球を大きく上回る値となっています。

タイタン

　次に、土星の衛星タイタンの大気での計算をしてみます。 タイタンは非常に濃い大気を持つ衛星として有名です。 タイタンの温度を 94 K、重力加速度を 1.354 m s^-2 とします。 タイタンの大気組成は、

• 窒素 95%
• メタン 4.9%

　スケールハイトを計算すると 21078.8281...m であり、タイタン大気のスケールハイトは ~ 21.1 km となります。

　静水圧平衡から導出した密度分布を \(z\) 方向に積分する事で、柱密度が計算出来ました。 また、柱密度に天体の表面積をかけることで大気の全質量を概算することができます。 柱密度 \(\Sigma\) と大気の全質量 \(\Matm\) は、それぞれ \begin{align*} \Sigma=\rho_{0}H_{0} \end{align*} \begin{align*} \Matm=4\pi R_{\rm p}\Sigma=\rho_{0}H_{0}\cdot 4\pi R_{\rm p} \end{align*} と表されます。 これらの式を用いて、さまざまな天体での大気の柱密度と、大気の全質量を計算してみます。

　スケールハイトは既に計算しましたが、柱密度を計算するためには表面での大気の密度が必要です。 そこで、理想気体の状態方程式より、 \begin{align*} \rho=\frac{M}{RT}P \end{align*} として計算します。 温度 \(T\)、平均モル質量 \(M\)、重力加速度 \(g\) は先程までと同じ値を用いて密度を計算します。

地球

　地球の場合、地表での大気密度と、大気の柱密度は
\(\rho_{0}\) = 1.23 kg m^-3
\(\Sigma\) = 1.03 × 10⁴ kg m^-2
となります。 ここで計算した柱密度の値から、1 平方メートルの地面の上に乗っている大気の質量はおおよそ 10000 kg、すなわち 1 平方メートルあたり 10 トンの大気が乗っているということが分かります。

　これに地球の表面積をかけると、地球大気の全質量は

\(\Matm\) = 5.27 × 10¹⁸ kg

と求まります。

　NASA の Earth Fact Sheet に掲載されている地球大気の全質量は 5.1 × 10¹⁸ kg となっており、おおむね一致していると言えます。 地球の質量は 5.9726 × 10²⁴ kg なので、地球大気の質量は地球質量のわずか 0.000088% ということになります。 大気層がいかに薄くわずかなものであるかが分かります。

火星

　火星の表面での大気圧は 6.36 hPa です。 地球の大気圧が 1013.25 hPa であることを考えると、非常に希薄な大気です。 ここから、火星の地表での大気密度と、大気の柱密度は
\(\rho_{0}\) = 1.58 × 10^-2 kg m^-3
\(\Sigma\) = 1.80 × 10² kg m^-2
と求められます。 火星の場合は、1 平方メートルあたりの大気質量は 180 kg であり、10 トンあった地球大気よりも遥かに小さい値になっています。

　これに火星の表面積をかけると、火星大気の全質量は

\(\Matm\) = 2.59 × 10¹⁶ kg

と求まります。 火星大気の質量は地球大気の質量の 0.49%、おおよそ 200 分の 1 程度の値になることが分かります。

　NASA の Mars Fact Sheet に掲載されている火星大気の全質量は 2.5 × 10¹⁶ kg となっており、こちらもおおむね一致していると言えます。 また、火星の質量は 0.64174 × 10²⁴ kg であるため、火星大気の質量は火星質量の 0.000004% ということになります。

金星

　金星の表面での大気圧は 92000 hPa です。 地球の大気圧のおよそ 90 倍の値であり、非常に高圧の環境になっています。 ここから、金星の地表での大気密度と、大気の柱密度は
\(\rho_{0}\) = 6.52 × 10 kg m^-3
\(\Sigma\) = 1.04 × 10⁶ kg m^-2
と求められます。 金星の場合は、1 平方メートルあたりの大気質量はおよそ 1000000 kg、つまり 1000 トンになります。 地球の場合は 10 トンだったため、およそ 100 倍となっています。

　柱密度に金星の表面積をかけると、金星大気の全質量は

\(\Matm\) = 4.77 × 10²⁰ kg

と求まります。 金星大気の質量は地球大気の質量の 90.5 倍となり、金星は地球の 90 倍の大気を持っていると言うことができます。

　NASA の Venus Fact Sheet に掲載されている金星大気の全質量は 4.8 × 10²⁰ kg となっており、こちらもおおむね一致していると言えます。 また、金星の質量は 4.8676 × 10²⁴ kg であるため、金星大気の質量は金星質量の 0.0098% ということになります。 地球や火星に比べて大気の量が遥かに多いため、大気質量の割合も他の天体に比べてずっと大きな値になっています。

タイタン

　タイタンの表面での大気圧はおよそ 1600 hPa です。 地球の大気圧よりも大きい値になっています。 ここから、タイタンの地表での大気密度と、大気の柱密度は
\(\rho_{0}\) = 5.26 kg m^-3
\(\Sigma\) = 1.11 × 10⁵ kg m^-2
と求められます。 タイタンの場合は、1 平方メートルあたりの大気質量は 111000 kg、おおむね 100 トンになるため、単位面積あたりの大気の量は地球の 10 倍だと分かります。

　タイタンの表面積をかけると、タイタン大気の全質量は

\(\Matm\) = 9.23 × 10¹⁸ kg

と求まります。 タイタンは地球よりずっと小さい衛星ですが、大気の全質量は地球の 1.75 倍となり、地球より多くの大気を持っていることが分かります。

　上のスケールハイト導出のときは、大気は等温であるという仮定をおきました。 そのため、状態方程式を微分した際に出てくる温度の \(z\) 微分の項は 0 になりました。 しかし実際には、大気の温度は高度に依存して変化します。 また、そのほかの物理量も常に一定である保証はありません。 そのため、一般的なスケールハイトは複雑な形になります。

　ここまでは、高度によって変化するのは密度と圧力だけだとして計算して来ました。 しかしより一般的には、理想気体の状態方程式は \begin{align*} P\!\left(z\right)=\frac{\rho\!\left(z\right)RT\!\left(z\right)}{M\!\left(z\right)} \end{align*} となります。 圧力と密度だけではなく、温度も \(z\) の関数となります。 また、平均モル質量も高度によって変化すると考えれば、\(z\) の関数として表す必要があります。 現実には、大部分の領域では平均モル質量は高度を通じて大きく変化はしませんが、高層大気では組成は大きく異なります。 気体定数 \(R\) は普遍定数であるため必ず一定です。 また、状態方程式は、 \begin{align*} P\!\left(z\right)=\frac{\rho\!\left(z\right)\kB T\!\left(z\right)}{\mu\!\left(z\right)\munit} \end{align*} と書く事も出来ます。 この表式では、平均モル質量の高度依存性の部分は平均分子量 \(\mu\) の高度依存性に変わっていますが、大気組成の高度依存性を表現している点は同じです。

　静水圧平衡の式は、より一般的には \begin{align*} \frac{dP}{dz}&=-\rho\!\left(z\right)g\!\left(z\right)\\ &=-\frac{M\!\left(z\right)g\!\left(z\right)}{RT\!\left(z\right)}P\!\left(z\right) \end{align*} と表されます。 2 行目で理想気体の状態方程式を代入しています。 重力加速度も厳密には高度の関数で、高度が高くなるほど小さくなるため \(z\) 依存性を持たせてありますが、大気の範囲内ではほとんど一定と見なせます。 この式を変形すると、 \begin{align*} \frac{1}{P\!\left(z\right)}\frac{dP}{dz}=\frac{M\!\left(z\right)g\!\left(z\right)}{RT\!\left(z\right)}\equiv\frac{1}{H\!\left(z\right)} \end{align*} となります。 ここで \(H\!\left(z\right)\) がスケールハイトであり、 \begin{align*} H\!\left(z\right)=\frac{RT\!\left(z\right)}{M\!\left(z\right)g\!\left(z\right)} \end{align*} となります。 スケールハイトは、温度・平均モル質量・重力加速度の関数になっており、これらは高度の関数であるため、結局はスケールハイトは高度の関数であることが分かります。 この式は、 \begin{align*} H\!\left(z\right)=\frac{\kB T\!\left(z\right)}{\mu\!\left(z\right)\munit g\!\left(z\right)} \end{align*} と書く事も出来ます。

　平均モル質量 (または平均分子量) と重力加速度の変化は無視出来るとした場合、スケールハイトは温度依存性を持つ値である事が分かります。 等温大気の仮定では、この温度依存性を無視して温度を定数として扱っているため、スケールハイトは高度依存性の無い定数として書くことができたということになります。

　静水圧平衡の式と、理想気体の状態方程式は同じものを用います。 ただし、温度の高度依存性を残したものを使います。 \begin{align*} \frac{dP}{dz}=-\rho\!\left(z\right)g \end{align*} \begin{align*} P\!\left(z\right)=\frac{\rho\!\left(z\right)RT\!\left(z\right)}{M} \end{align*} 重力加速度については、大気の範囲内では変化は無視出来るため定数として扱います。 また、同じく大気組成に関しても一定であると仮定し、平均モル質量を定数としています。

　ここで温度の高度依存性を、次のような形で与えます。 \begin{align*} T\!\left(z\right)=T_{0}-\Gamma z \end{align*} \(T_{0}\) は地表面での温度です。 \(\Gamma\) は高度による温度の低下度合いを表す定数で、温度を長さで割った次元 (例えば [K m^-1]) を持っており、気温減率 (temperature lapse rate) と呼ばれます。 つまりここでは、地表での温度が \(T_{0}\) で、そこから \(\Gamma\) の割合で温度が低下して行くという大気を仮定しているということになります。

　理想気体の状態方程式と温度の高度依存性の式を、静水圧平衡の式に代入することで以下の式が得られます。 \begin{align*} \frac{dP}{dz}=-\frac{Mg}{R\left(T_{0}-\Gamma z\right)}P \end{align*} これを変形して変数分離形にすると、 \begin{align*} \frac{dP}{P}=-\frac{Mg}{R\left(T_{0}-\Gamma z\right)}dz \end{align*} となります。

　ここで、 \begin{align*} F\!\left(x\right)=\int\frac{dx}{ax+b} \end{align*} という不定積分を考えます。 ここで、\(t=ax+b\)、\(dt=a\,dx\) と変数変換をすれば、 \begin{align*} F\!\left(x\right)=\int\frac{1}{at}dt=\frac{1}{a}\ln\abs{t}+C=\frac{1}{a}\ln\abs{ax+b}+C \end{align*} と積分することができます。 \(C\) は積分定数です。 この結果を利用して、圧力に関する微分方程式は以下のように積分することができます。 \begin{align*} \ln\abs{P}=\frac{Mg}{R\Gamma}\ln\abs{T_{0}-\Gamma z}+C^{\prime} \end{align*} \(C^{\prime}\)は積分定数です。 ここで、右辺にある係数 \(\displaystyle{\frac{Mg}{R\Gamma}}\) は無次元量になっている事が容易に確かめられます。 そこで、この係数を \begin{align*} \alpha=\frac{Mg}{R\Gamma} \end{align*} と置いておきます。 これを用いると、式は \begin{align*} \ln\abs{P}=\ln\abs{T_{0}-\Gamma z}^{\alpha}+C^{\prime} \end{align*} と書くことができます。 この式の両辺の対数を外してやる事で、 \begin{align*} P\!\left(z\right)=C\left(T_{0}-\Gamma z\right)^{\alpha} \end{align*} となります。 \(C\) は同じく積分定数です。

　ここで境界条件から積分定数を決定する事を考えます。 上で行ったスケールハイトの導出の時と同様に、地表面、すなわち \(z=0\) で圧力は \(P_{0}\) であるとすると、 \begin{align*} P_{0}=CT_{0}^{\alpha} \end{align*} になるため、積分定数は \(C=P_{0}/T_{0}^{\alpha}\) となります。 よって、圧力構造の式は以下のようになります。 \begin{align*} P\!\left(z\right)=\frac{P_{0}}{T_{0}^{\alpha}}\left(T_{0}-\Gamma z\right)^{\alpha}=P_{0}\left(1-\frac{\Gamma}{T_{0}}z\right)^{\alpha} \end{align*}

　一方、理想気体の状態方程式に圧力構造の式を代入する事によって、密度構造を以下のように求めることができます。 \begin{align*} \rho\!\left(z\right)&=\frac{M}{RT\!\left(z\right)}P\!\left(z\right)\\ &=\frac{M}{R\left(T_{0}-\Gamma z\right)}P_{0}\left(1-\frac{\Gamma}{T_{0}}z\right)^{\alpha}\\ &=\frac{MP_{0}}{RT_{0}}\left(1-\frac{\Gamma}{T_{0}}z\right)^{\alpha-1} \end{align*} ここで、\(z=0\) の時の理想気体の状態方程式は \begin{align*} P_{0}=\frac{\rho_{0}RT_{0}}{M} \end{align*} となる事を考えると、\(\displaystyle{\rho_{0}=\frac{MP_{0}}{RT_{0}}}\) と書くことができます。

　以上より、次の結果が得られます。

等温大気との比較

高度依存性

　等温大気の場合は、圧力構造は \begin{align*} P\!\left(z\right)=P_{0}\exp\left(-\frac{z}{H_{0}}\right) \end{align*} 密度構造は \begin{align*} \rho\!\left(z\right)=\rho_{0}\exp\left(-\frac{z}{H_{0}}\right) \end{align*} と、全く同じ依存性を持っていました。

　しかし等温でない場合は、形は似ているものの指数が 1 だけ違っています。 そのため、非等温大気の場合は圧力と密度の高度依存性は異なることが分かります。

　また、等温大気の場合は指数関数的に減衰していますが、この非等温大気の場合は指数関数ではなくべき関数的になっています。

大気上端の存在

　等温大気の場合は指数関数的な減衰になっているため、圧力や大気は無限遠の高度で0になる構造になっています。 しかし非等温大気の場合は、式の形より \(z=T_{0}/\Gamma\) の時に圧力・密度ともに 0 になります。

　従って、非等温大気では有限の高度で圧力・密度が 0 になるということが分かります。 今考えている問題設定の下では、地表での温度と気温減率から大気の上端が決まります。

　地表面の温度が高ければ大気の上端は高くなり、気温減率が大きく温度の減少が大きい場合は大気の上端は低くなります。

スケールハイト

　一般的な条件でのスケールハイトは、 \begin{align*} H\!\left(z\right)=\frac{RT\!\left(z\right)}{M\!\left(z\right)g\!\left(z\right)} \end{align*} で与えられるのでした。 従って、今考えている状況ではスケールハイトは \begin{align*} H\!\left(z\right)=\frac{R\left(T_{0}-\Gamma z\right)}{Mg} \end{align*} となり、高度の関数になっています。 スケールハイトも圧力・密度と同様に、\(z=T_{0}/\Gamma\) で 0 となります。 温度の高度依存性の式から、\(z=T_{0}/\Gamma\) では温度が 0 になります。 そのため、結局これらの式は温度が 0 になる所で圧力・密度・スケールハイトは 0 になり、大気がそこで途切れているという自明な事を表しています。

　このスケールハイトの式に、\(z=0\) を代入すると \begin{align*} H\!\left(0\right)=H_{0}=\frac{RT_{0}}{Mg} \end{align*} となり、等温大気のスケールハイトと同じ形になっています。 よって、等温大気のスケールハイトと非等温大気のスケールハイトは、地上 (\(z=0\)) では一致します。

上空での圧力の具体値

　非等温大気での圧力構造の式 \begin{align*} P\!\left(z\right)=P_{0}\left(1-\frac{\Gamma}{T_{0}}z\right)^{\alpha} \end{align*} に具体的な値を代入して、上空での密度を計算してみます。 問題になるのは気温減率の値ですが、ここでは平均的な気温減率を計算に用いる事にします。 登山などの時に、「標高が 100 m 上がるごとに気温は 0.6℃ 下がる」というのを聞いた事があるかもしれません。 100 m 上昇するごとに 0.6 K の温度低下があるということなので、この場合の気温減率は、Γ = 0.006 K m^-1 となります。 ここではこの値を用いる事にします。

　地表での大気圧を \(P_{0}\) = 1013.25 hPa、\(T_{0}\) = 288 K とし、平均モル質量や重力加速度もこれまで用いたものと同じ値を代入します。 このとき、富士山山頂の \(z\) = 3776 m での気圧は 640 hPa、エベレスト山頂の \(z\) = 8848 m での気圧は 324 hPa となります (等温大気の場合はそれぞれ 648 hPa、355 hPa)。 大きな差ではありませんが、温度の依存性を考えることによって値が変わっていることが分かります。 特にエベレスト頂上での値は、一般的に言われている「地上の 3 分の 1」という値により近くなっています。

　なお、この仮定のもとで、圧力が 0 になる高度 \(z=T_{0}/\Gamma\) を計算すると、 288 [K] / 0.006 [K m^-1] = 48 [km] となります。 つまり高度 48 km の地点で大気が途切れるということになります。 もちろん実際はそのような事にはなっていません。 地球大気はいくつかの層に分かれており、高度が上がるに従って気温が下がっていく対流圏は、高度 11 km 程度まで続いています。 そこより上は成層圏ですが、そこでは気温は高度につれて低下せず、むしろ上昇する傾向にあります。 そのため、温度が高度に従って一定の割合で低下して行くという仮定は、高度 11 km 程度より上空では間違っているということになります。

大気の柱密度と大気の全質量

　密度構造の式を \(z\) 方向に積分すると大気の柱密度が計算でき、そこから大気の全質量が計算出来ることは既に紹介しました。 先程で計算した非等温大気の場合も大気の密度構造が導出出来たため、これを \(z\) 方向に積分する事で同じ議論が出来るはずです。 ここまでの議論から、大気は \(z=T_{0}/\Gamma\) で途切れることが分かっています。 よって積分の上端は無限遠ではなく \(z=T_{0}/\Gamma\) までという事になり、柱密度は以下の積分から計算出来ることになります。 \begin{align*} \Sigma=\int_{0}^{T_{0}/\Gamma}\rho_{0}\left(1-\frac{\Gamma}{T_{0}}\right)^{\alpha-1}dz \end{align*} 簡単の為に、\(\displaystyle{X=1-\frac{\Gamma}{T_{0}}z}\)、\(\displaystyle{dX=-\frac{\Gamma}{T_{0}}dz}\) と変数変換をすると、 \begin{align*} \Sigma&=-\frac{\rho_{0}T_{0}}{\Gamma}\int_{1}^{0}X^{\alpha-1}dX=\frac{\rho_{0}T_{0}}{\Gamma}\int_{0}^{1}X^{\alpha-1}dX\\ &=\frac{\rho_{0}T_{0}}{\Gamma\alpha} \end{align*} となります。

　\(\displaystyle{\alpha=\frac{Mg}{R\Gamma}}\) を代入すれば、柱密度は \begin{align*} \Sigma=\frac{\rho_{0}RT_{0}}{Mg} \end{align*} となります。 ここで先程紹介した地表面でのスケールハイト \(\displaystyle{H\!\left(0\right)=H_{0}=\frac{RT_{0}}{Mg}}\) を用いると、 \begin{align*} \Sigma=\rho_{0}H_{0} \end{align*} と書け、等温大気の仮定で導出した柱密度と全く同じになることが示せました。

　大気が等温である事を仮定すると、密度と圧力は指数関数的な減少をし、大気が非等温であり、一定の割合で温度が下がって行く大気を仮定すると、密度と圧力はべき関数的に下がって行くことが分かりました。 また、適切と思われる気温減率を仮定して実際の圧力を計算した結果、小さなずれはあるもののおおむね近い値になる事も分かりました。

　両者の違いは温度構造のみであり、等温大気は温度は地上の温度で常に一定、非等温大気の場合はここでは \(T\!\left(z\right)=T_{0}-\Gamma z\) という構造を仮定しました。 この場合、気温減率が 0 のときが等温大気であるということになります。 そのため気温減率が小さい極限(\(\Gamma\rightarrow0\))では、非等温大気の構造は等温大気の構造に漸近するはずです。 ここではそれを確かめてみます。

　大気の温度が \(T\!\left(z\right)=T_{0}-\Gamma z\) で与えられる場合の圧力構造は \begin{align*} P\!\left(z\right)=P_{0}\left(1-\frac{\Gamma}{T_{0}}z\right)^{\alpha} \end{align*} でした。 ただし、\(\displaystyle{\alpha=\frac{Mg}{R\Gamma}}\) です。 \(\Gamma\) を 0 に近付けると、括弧の中は 1 に近付きますが、指数の分母にも \(\Gamma\) が入っているため指数は無限大に発散してしまいます。 そのため、ちゃんと極限を取って考えてやる必要があります。 ここでは、 \begin{align*} \lim_{\Gamma\rightarrow0}\left(1-\frac{\Gamma}{T_{0}}z\right)^{Mg/R\Gamma} \end{align*} を計算します。

　ここで、 \begin{align*} \frac{\Gamma}{T_{0}}z=\frac{1}{X} \end{align*} と変数変換をすると、極限は \begin{align*} \lim_{\Gamma\rightarrow0}\left(1-\frac{\Gamma}{T_{0}}z\right)^{Mg/R\Gamma}&=\lim_{X\rightarrow\infty}\left(1-\frac{1}{X}\right)^{MgzX/RT_{0}}\\ &=\lim_{X\rightarrow\infty}\left[\left(1-\frac{1}{X}\right)^{X}\right]^{Mgz/RT_{0}} \end{align*} と書き換えることができます。

　この極限の形は、高校数学で扱った通り、以下のように計算出来ます。 \begin{align*} \lim_{x\rightarrow\infty}\left(1-\frac{1}{x}\right)^{x}&=\lim_{x\rightarrow\infty}\left[\frac{1}{\frac{x}{x-1}}\right]^{x}\\ &=\lim_{x\rightarrow\infty}\left[\frac{1}{1+\frac{1}{x-1}}\right]^{x}\\ &=\lim_{x\rightarrow\infty}\left[\frac{1}{1+\frac{1}{x-1}}\right]^{x-1}\left[\frac{1}{1+\frac{1}{x-1}}\right]\\ &=\lim_{t\rightarrow\infty}\frac{1}{\left(1+\frac{1}{t}\right)^{t}}\frac{1}{\left(1+\frac{1}{t}\right)}\\ &=\frac{1}{e}\frac{1}{1}=e^{-1} \end{align*}

　この結果を用いると、 \begin{align*} \lim_{X\rightarrow\infty}\left[\left(1-\frac{1}{X}\right)^{X}\right]^{Mgz/RT_{0}}=\left(e^{-1}\right)^{Mgz/RT_{0}}=e^{-Mgz/RT_{0}} \end{align*} と書き換えられます。 また、地表でのスケールハイトが \begin{align*} H\!\left(0\right)=H_{0}=\frac{RT_{0}}{Mg} \end{align*} と表される事を利用すると \(e\) の指数の部分は \(-z/H_{0}\) に書き換えられるため、最終的に \begin{align*} \lim_{\Gamma\rightarrow0}P_{0}\left(1-\frac{\Gamma}{T_{0}}z\right)^{Mg/R\Gamma}=P_{0}\exp\left(-\frac{z}{H_{0}}\right) \end{align*} となります。

　よって、気温減率が 0 となる極限では、非等温大気の構造は等温大気の構造と一致することが証明出来ました。

　等温の大気構造と、非等温の大気構造をグラフにして比較をしてみます。

　横軸が地表面からの高度 [km]、縦軸が気圧 [hPa] です。 地表面での圧力は \(P_{0}\) = 1013.25 hPa とし、地上での温度 \(T_{0}\) = 288 K、気温減率 \(\Gamma\) = 0.006 K m^-1 としています。 平均モル質量や重力加速度は地球大気の計算の際に上で用いたものと同じ値を使っています。 赤で示したのが等温大気で、指数関数的な減衰をするものです。 緑で示したものが非等温大気で、べき関数的な減衰をするものです。

　地表付近では両者の違いはあまり大きくありません。 富士山山頂とエベレスト山頂での違いを比較しましたが、どちらも高度 10 km 未満であるためこのグラフ上では違いがほとんど見えない領域です。 しかし高度が上がるにつれて違いが顕著になって行きます。

　また、等温大気の場合は圧力は 0 に漸近しますが、有限の高度では 0 になりません。 それに対して、非等温大気の場合は途中で 0 になっています。 先程の議論から、表面での温度が 288 K、気温減率が 0.006 K m^-1 の場合は高度 48 km で圧力が 0 になるのでした。 そのあたりでちゃんと圧力が 0 になっている事が確認出来ます。

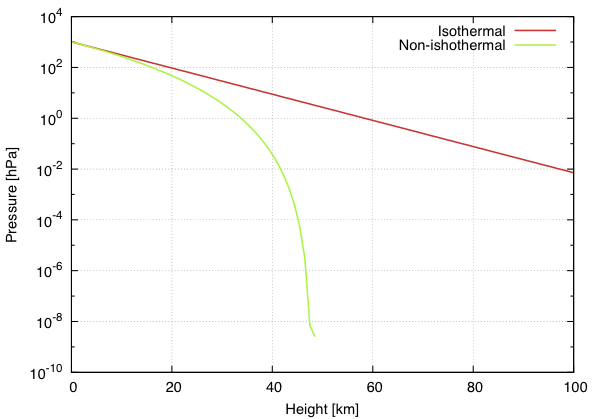
　上のグラフでは減少が急激で見づらいため、縦軸の対数を取ったグラフを表示します。

　上のものと同じデータですが、縦軸が対数目盛になっています。 そのため、指数関数である等温大気 (赤) は直線になっています。 また、非等温大気 (緑) が 48 km の所で 0 になっている (縦軸が対数のため、グラフ上では無限小に発散する) ことが分かります。
　地上付近では等温大気と非等温大気のずれは非常に小さいですが、高度が高くなると一気にずれが大きくなります。 逆に言うと、地上付近では等温大気の仮定はおおむね正しいと言えるということでもあります。

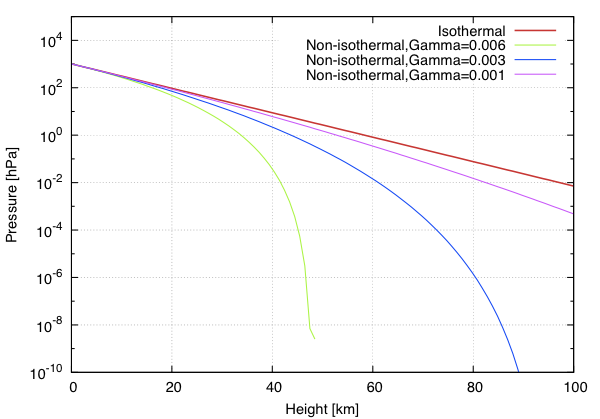
　気温減率が 0 の極限では、非等温大気と等温大気は一致することを示しました。 そこで、気温減率の値を変えた場合の大気の圧力構造を比較してみます。

　赤が等温大気です。 緑で示したのが先程と同じで気温減率が \(\Gamma\) = 0.006 K m^-1 の場合、青が \(\Gamma\) = 0.003 K m^-1、マゼンタが \(\Gamma\) = 0.001 K m^-1 の場合です。 気温減率が小さい場合は温度が 0 になる高度が高いため、大気が途切れる位置も高くなっていることが分かります。 また、気温減率を小さくするほど、赤の等温大気の線に漸近して行く事も分かります。

参考文献